Teorik Detayı ile Yan-Varyans İkilemi

Uygulamada gerek zaman gerekse maliyetin büyük olması nedeniyle tüm kitle (population) birimlerin incelenmesi olanaklı olmayabilir. Bu durumda kitleden örnekleme yöntemleri yardımıyla kitleyi en iyi şekilde temsil edecek büyüklükte, ancak kitlenin büyüklüğünden daha az sayıda rastgele seçilen birimlerin oluşturduğu topluluğa örneklem (sample) adı verilir. Örneklemin elde edilme sürecine örnekleme (sampling) denir.

Kitle ya da örneklemde her alan her birime denek (subject) ya da gözlem (observation) denir. Kitle ya da örneklemdeki denek değerleri ya da gözlem değerleri verileri (data) oluşturur.

Kitleyi temsil eden, sayısal değerlere parametre (parameter) denir. Örneğin, kitlenin ortalaması $\mu$ ve varyansı $\sigma^2$ birer parametrelerdir. Bu parametreler üzerinde çalıştığımız değişken için kitle hakkında bilgi verir.

Yukarıda da belirtildiği gibi, tüm kitle birimlerinin incelenmesi her zaman mümkün değildir. Bu nedenle, örnekleme yöntemleri (sampling methods) ile bu kitleyi en iyi şekilde temsil eden bir örneklem seçeriz. Örneklemin kitleyi iyi bir şekilde temsil etmesi, örnekleme yönteminin doğru seçilmesine bağlıdır ve istatistiksel çıkarsamaların güvenilirliği açısından çok önemlidir. Kitle parametresini örneklemden tahmin etmek için kullanılan istatistiğe tahmin edici (estimator), bu istatistiğin örneklemden hesaplanan değerine tahmin (estimate) denir. Örneğin, kitle ortalama $\mu$ ve onun örneklemeden tahmin edicisi $\bar{X}$ ve bu tahmin edicinin tahmini $\bar{x}$ (tahminin küçük harf ile yazıldığına dikkat edelim!).

Bu örneklemi kullanarak kitle hakkında bilgi sahip olmak için istatistiksel çıkarsama (statistical inference) gerçekleştiririz. İstatistiksel çıkarsama, örneklem özelliklerden kitle özelliklerini çıkardığımız süreçtir ve bilinmeyen kitle parametrelerini tahmin etmektir. İstatistiksel çıkarsamanın iki türü vardır: (1) Tahmin ve (2) Hipotez Testleri. Bu iki kavram aslında birbirine çok benzerdir. Ancak, bu yazı boyunca daha çok Tahmin ile ilgileneceğiz.

Tahminin amacı, bir örneklemden elde edilen tahmin ediciyi (estimator), bir kitle parametresinin değerini yaklaşık olarak tahmin etmektir. Örneğin, örneklem ortalaması olan $\bar{X}$, kitle ortalaması olan $\mu$’nün bir tahmin edicisidir.

İki türlü tahmin yapılabilir:

1. Nokta Tahmini (Point Estimation): Bir nokta tahmin edicisi, tek bir değer kullanarak bilinmeyen bir parametrenin değerini tahmin ederek bir kitle hakkında çıkarımlar yapar.

1. Aralık Tahmini (Interval Estimation): Bir aralık tahmincisi, bilinmeyen bir parametrenin değerini bir aralık ile tahmin ederek bir kitle hakkında çıkarımlar yapar. Burada, gerçek kitle parametresini belirli bir olasılıkla “kapsayan” bir aralık oluşturmaya çalışırız.

Ancak burada dikkat edilmesi gereken nokta, kitle parametresinin sadece bir tane örneklem üzerinden tahmininin gerçekleşmemesidir.

Üzerinde çalıştığımız değişken için kitlede bir parametre $\theta$ olsun ve bir örneklemden elde edilen tahmin edici ise $\hat{\theta}$ ile gösterilsin. Kitleden aynı büyüklükte çok sayıda rastgele örneklemler seçildiğinde, örneklemlerin her birinde bulunan tahminler farklı olmaktadır. Bunun nedeni, kitleden rastgele seçilen örneklem birimlerinin her bir örneklem için farklı olmasıdır, yani, $k$ tane örneklem seçtiğimizi varsayarsak ve seçilen bu her bir örneklem için $\theta$ parametresini tahmin ediyorsak, elimizde, $\hat{\theta_{1}}, \hat{\theta_{2}}, \cdots, \hat{\theta_{k}}$ var demektir. Başka bir deyişle, kitle parametresini örneklemden tahmin etmek için kullanılan tahmin edici, bir raslantı değişkenidir ve bir dağılıma sahiptir. Bu istatistiğin olasılık dağılımına örnekleme dağılımı (sampling distribution) adı verilir.

Örnekleme dağılımının elde edilmesi

Bir örnekleme dağılımı, kitlenin büyüklüğüne, örneklemin büyüklüğüne ve örneklem seçme yöntemine bağlıdır. Bir istatistiğin örnekleme dağılımını elde etmek için aşağıdaki yol izlenir:

1. Önce çıkarsama yapılacak olan kitle parametresi belirlenir. En sık başvurulan parametreler, kitle ortalaması, kitle varyansı ya da belirli bir özelliğe sahip olan birimlerin kitledeki oranıdır.
2. $N$ birimlik kitleden $n$ büyüklüğündeki tüm örneklemler seçilir ve ilgilenilen parametreye karşılık gelen örneklem istatistiğinin değeri, her bir örneklem için hesaplanır. Kitle birimleri her seferinde yerine konularak örneklem seçiliyorsa, tüm mümkün örneklem sayısı $N^{n}$ olur. Kitle birimleri yerine konulmadan örneklem seçiliyorsa, tüm mümkün örneklem sayısı $\binom{N}{n}$ olur.
3. İkinci adımda örneklemlerden elde edilen istatistiklerin değerleri için sıklıklar hesaplanır. Elde edilen sıklık ya da göreli sıklıkların dağılımı, ilgili istatistiğin örnekleme dağılımı olacaktır.

İkinci şıkta belirtilen tüm olası örneklemlerin sayısı (yerine koyarak ya da yerine koymadan) kitlenin kendisinden daha büyüktür. Bu nedenle örnekleme dağılımının bu şekilde oluşturulması kitlenin kendisini gözlemlemekten daha zor bir iştir. Kitle sonsuz büyüklükte olduğunda bu işlem olanaksızdır. Uygulamada $N$ büyüklüğündeki bir kitleden $n$ büyüklüğündeki tüm örneklemleri seçmek olanaksız olduğundan $k$ sayıda örneklem seçilir. İlgilenilen parametreye karşılık gelen örneklem istatistiğinin değeri her bir örneklem için hesaplanır. Bu şekilde $k$ örneklemin istatistiklerinden oluşan yeni bir örneklem elde edilir. Bu örneklemin dağılımı, örnekleme dağılımı olarak isimlendirilir.

Örnekleme Ortalaması olan $\overline{X}$’ın Örnekleme Dağılımının Elde Edilmesi

Örneğin, örneklem ortalaması $\overline{X}$ için süreç şu şekilde işler. Sonlu bir kitle için yukarıdaki süreç uygulanarak örneklem ortalamasının örnekleme dağılımı elde edilebilir. $N$ büyüklüğündeki kitleden $n$ büyüklüğündeki tüm örneklemler çekilir, her bir örneklemin ortalaması hesaplanır ve ortalamaya karşılık gelen sıklık ve göreli sıklık dağılımı elde edilir. Bu göreli sıklık dağılımı, örneklem ortalamasının örnekleme dağılımıdır.

Bu dağılımın ortalaması ve varyansı, yerine koymadan yapılan örnekleme için,

\[\mathbb{E}(\overline{X}) = \mu\]

ve

\[V(\overline{X})=\sigma_{\overline{\mathrm{X}}}^{2}=\frac{\sigma^{2}}{\mathrm{n}}\left(\frac{N-n}{N-1}\right)\]

şeklindedir. Bu formüllerin nasıl bulunduğu burada bulunan dökümanda görülebilir.

Benzer şekilde, yerine koyarak yapılan örnekleme için örneklem ortalamasının beklenen değeri,

\[\begin{split} \mathbb{E}(\overline{X}) &= \mathbb{E}\left(\dfrac{X_1 + X_2 + \dots + X_n}{n}\right) \\ &= \dfrac{1}{n}\, \mathbb{E}(X_1 + X_2 + \dots + X_n) \\ &= \dfrac{1}{n}\, \bigl(\mu + \mu + \dots + \mu\bigr) \\ &= \dfrac{1}{n}\, n\mu \\ &= \mu. \end{split}\]

ve varyansı

\[\begin{split} \operatorname{Var}(\overline{X}) &= \mathrm{var}\left(\dfrac{X_1 + X_2 + \dots + X_n}{n}\right) \\ &= \Bigl(\dfrac{1}{n}\Bigr)^2\, \mathrm{var}(X_1 + X_2 + \dots + X_n) \\ &= \Bigl(\dfrac{1}{n}\Bigr)^2\, \bigl(\sigma^2 + \sigma^2 + \dots + \sigma^2\bigr) \quad (X_i\text{'ler bağımsız oldukları için}) \\ &= \Bigl(\dfrac{1}{n}\Bigr)^2\, n\sigma^2 \\ &= \dfrac{\sigma^2}{n} \end{split}\]

formülleri ile elde edilir.

Yan ve Varyans

Peki, kitle parametresi $\theta$ için örneklemden elde ettiğimiz tahmin edici $\hat{\theta}$’in ne kadar iyi olduğunu nasıl ölçebiliriz? İstatistiksel ölçümler için iki “iyilik (goodness)” ölçüsü kullanılır:

1. Yan (Bias): Yan hesaplaması gerçekleştirirken cevaplamaya çalıştığımız soru “Bir tahmin edici için elde edilen tahmin, bu tahmin edicinin gerçek değerine ne kadar yakın?” sorusudur.
2. Varyans (Variance): Varyans hesaplaması gerçekleştirirken cevaplamaya çalıştığımız soru ise “farklı çalıştırmalar (yani farklı örneklemler veya farklı veri kümeleri) için elde edilen bu tahmin ne kadar değişir”dir.

Yukarıda dediğimiz gibi kitle parametresini örneklemden tahmin etmek için kullanılan tahmin edici, bir raslantı değişkenidir ve bir dağılıma sahiptir. Bu dağılımı aşağıdaki gibi bir grafik ile gösterdiğimizde, yan ve varyans konseptleri daha iyi anlaşılacaktır:

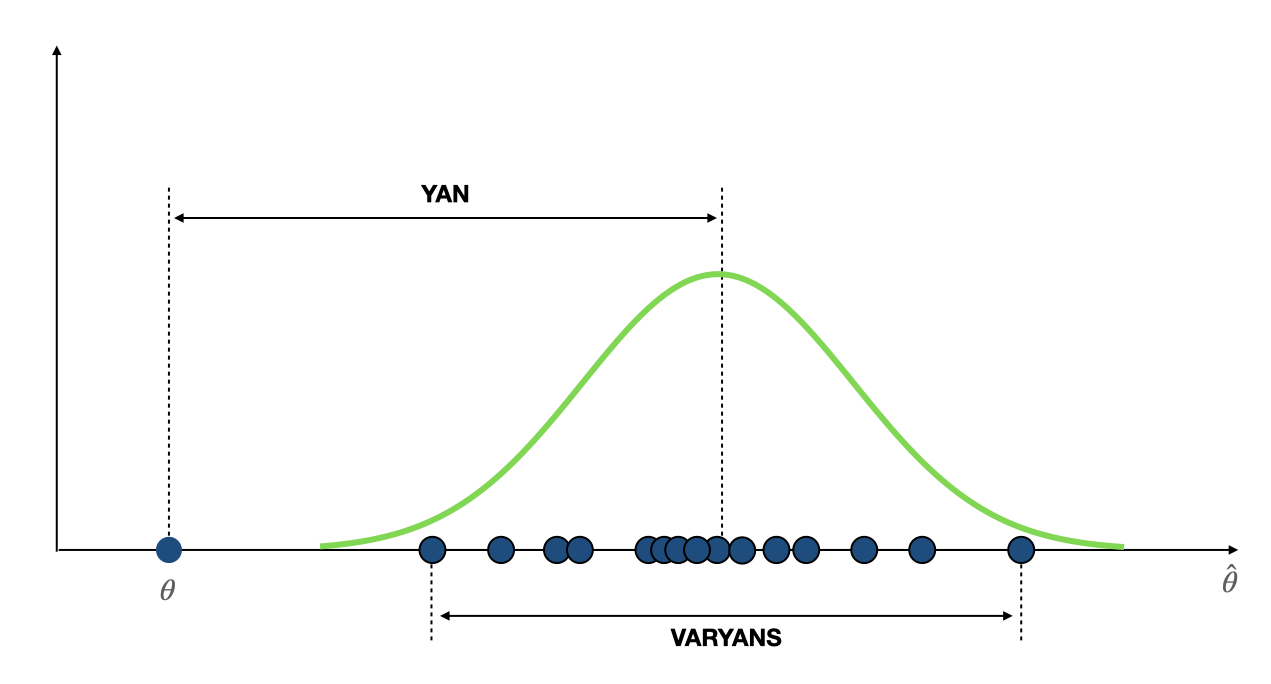
Matematiksel olarak, yan, $\operatorname{bias}(\hat{\theta})= \mathbb{E}(\hat{\theta})-\theta$ ile hesaplanır. Eğer, bir tahmin edici yansız ise, $\operatorname{bias}(\hat{\theta}) = 0$ olacaktır. Yani, $\mathbb{E}(\hat{\theta}) = \theta$. Örneğin, yukarıda da gösterildiği gibi, örneklem ortalaması $\bar{X}$, kitle parametresi $\mu$’nün yansız bir tahmin edicisidir. Çünkü $\mathbb{E}(\bar{X}) = \mu$ elde edilmiştir.

Bir rastlantı değişkeninin varyansı, bu rastlantı değişkeninin, ortalamasından ayrılışının karesinin beklenen değeridir. Bir tahmin edici de bir rastlantı değişkeni olduğu için varyansını benzer şekilde hesaplayabiliriz. Yani, $\mathbb{E}\left((\hat{\theta} - \mathbb{E}(\hat{\theta}))^{2}\right)$. Örneğin, yukarıda da gösterildiği gibi, örneklem ortalamasının varyansı $\mathbb{E}\left((\bar{X}-\mathbb{E}(\bar{X}))^{2}\right)$ ile hesaplanır. Burada örneklem ortalamasının beklenen değeri kitle ortalamasına eşit olduğundan (yani $\mathbb{E}(\bar{X}) = \mu$), $\mathbb{E}\left((\bar{X}-\mathbb{E}(\bar{X}))^{2}\right)= E\left((\bar{X}-\mu)^{2}\right)$ yazılabilir.

$\mathbb{E}\left((\bar{X}-\mathbb{E}(\bar{X}))^{2}\right) = \mathbb{E}\left((\bar{X}-\mu)^{2}\right)$ eşitliğini açtığınızda ve gerekli işlemleri yaptığınızda yukarıda verilen $\mathrm{Var}(\overline{X})$’i elde etmeniz gerekmektedir. $\mathbb{E}(X^2) = \mathbb{E}(X)]^2 + \operatorname{Var}(X)$ olduğunu bildiğimize göre:

\[\begin{align*} \mathbb{E}((\overline{X} - \mu)^2) &= [\mathbb{E}(\overline{X} - \mu)]^2 + \text{Var}(\overline{X} - \mu) \\ &= \text{Var}(\overline{X}) \\ &= \text{Var}\left(\frac{1}{n}(X_1 + \cdots + X_n) \right) \\ &= \frac{n\sigma^2}{n^2}\\ &= \dfrac{\sigma^2}{n} \end{align*}\]

elde edebiliriz.

Yan ve Varyans İlişkisi

Bir $\theta \in R$ parametresini tahmin etme durumunu ele alalım ve $\hat{\theta}$ tahmininin hatasını gerçek $\theta$ parametresine kıyasla analiz etmek istediğimizi varsayalım. Bu hatayı karakterize etmenin birkaç yolu vardır. Matematiksel ve hesaplamalı nedenler yüzünden popüler bir seçim kare kaybıdır (squared loss). Tahmin ve gerçek parametre arasındaki hata şu şekilde ölçülür: $\mathbb{E} \left((\hat{\theta}-\theta)^{2}\right)$. Burada $\mathbb{E}(\cdot)$ beklenen değerdir.

Biraz matematik yaparak, bu hata ölçüsünün doğasını daha iyi tanımlayabiliriz. Sahip olduğumuz şey:

\[\begin{aligned} \mathbb{E}\left((\hat{\theta}-\theta)^{2}\right) &= \mathbb{E}\left((\hat{\theta} - \mathbb{E}(\hat{\theta}) + \mathbb{E}(\hat{\theta})-\theta)^{2}\right) \\ &=\mathbb{E}\left((\mathbb{E}(\hat{\theta})-\theta)^{2}\right) + \mathbb{E}\left((\hat{\theta} - \mathbb{E}(\hat{\theta}))^{2}\right)+2 \mathbb{E}((\mathbb{E}(\hat{\theta})-\theta)(\hat{\theta}-\mathbb{E}(\hat{\theta}))\\ &=\mathbb{E}\left((\mathbb{E}(\hat{\theta})-\theta)^{2}\right)+\mathbb{E}\left((\hat{\theta}-\mathbb{E}(\hat{\theta}))^{2}\right)+2(\mathbb{E}(\hat{\theta})-\theta)(\mathbb{E}(\hat{\theta})-\mathbb{E}(\hat{\theta})) \\ &=\mathbb{E}\left((\mathbb{E}(\hat{\theta})-\theta)^{2}\right)+\mathbb{E}\left((\hat{\theta}-\mathbb{E}(\hat{\theta}))^{2}\right) . \end{aligned}\]

Burada, $\mathbb{E}\left((\hat{\theta}-\mathbb{E}(\hat{\theta}))^{2}\right)$ teriminin $\hat{\theta}$ tahmin edicisinin varyansı olduğu kolaylıkla anlaşılabilir. Diğer terim $\mathbb{E}\left((\mathbb{E}(\hat{\theta})-\theta)^{2}\right)$, “en iyi” tahminin gerçek değerden ne kadar uzakta olduğunu ölçer. Yan terimini, $\operatorname{bias}(\hat{\theta})= \mathbb{E}(\mathbb{E}(\hat{\theta})-\theta)$ ile tanımlamak oldukça yaygındır. Bu notasyonu kullanarak

\[\mathbb{E}\left(\left(\hat{\theta}-\theta \right)^{2}\right)=\left[\operatorname{bias}(\hat{\theta})\right]^{2}+\operatorname{Var}(\hat{\theta})\]

elde ederiz.

Bu denklem, beklenen tahmin hatasının (kare kaybı ile ölçüldüğü gibi) yan’ın karesi, artı varyansa eşit olduğunu ve aslında bir tahmin edici için bu iki konsept arasında bir denge olduğunu belirtir.

Burada 3 yorum yapabiliriz:

1. $\operatorname{bias}(\hat{\theta})= \mathbb{E}(\mathbb{E}(\hat{\theta})-\theta) = 0$ olduğunda bu tahmin ediciye yansız (unbiased) tahmin edici denir.
2. Yan-Varyans dengesi, parametrik olmayan tahminlerde ve diğer modellerde vektör değerli parametreler $\theta \in R$ için mevcuttur.
3. Aşırı uyum (overfitting) terimi bazen düşük yanlı ama çok yüksek varyansa sahip bir modele atıfta bulunmak için kullanılır. Benzer şekilde, yetersiz uyum (underfitting) terimi, hem düşük yanlı hem de düşük varyanslı modeller için kullanılır.

Peki, bu bilgi Makine Öğrenmesindeki Yan-Varyans İkilemi (Bias-Variance Tradeoff) ile nasıl ilişkilidir.

Yan-Varyans İkilemi

Tahmine dayalı modellemede (yukarıdaki şekilde gösterildiği gibi), geçmiş verilere dayalı olarak bir denetimli model eğitir ve ardından önceden görülmemiş verileri tahmin etmek için bu eğitilmiş modeli kullanırız. Bu süreçte, model, hedef değişken (target variable) ile girdi öznitelikleri (input features) arasındaki ilişkiyi öğrenir. Bu ilişki $y=f(x)+\varepsilon$ gibi bir fonksiyon ile tanımlanabilir. Bu fonksiyona eşleme fonksiyonu (matching function) denir.

Bu durumu kolay anlaşılması açısından bir regresyon örneği ve Ortalama Kare Hata (Mean Squared Error - MSE) maliyet fonksiyonunu (cost function) kullanarak gösterelim.

Bazı temel kavramları tanımlayarak başlayalım. Deterministik veya deterministik olmayan bir ilişki yoluyla bağımlı değişken $y$’nin değerini etkileyen $x$ bağımsız değişkenlerimiz olduğunu varsayıyoruz. Deterministik olmayan diyoruz çünkü y’nin değeri açıkça modellenemeyen gürültüden de etkilenebilir. $x$ ve $y$ arasındaki gerçek ilişkiyi temsil eden $f$ fonksiyonu aracılığıyla $y$’nin $x$’e bağımlılığını gösterelim. Gerçek durumlarda, bu ilişkiyi bilmek elbette çok zor - imkansız değilse de - ama $f$’nin bilinmediği (unknown) zaman bile sabit (fixed) olduğunu varsayacağız. Bu durumda $x$ ve rastgele gürültünün birleşimi olan $y$ aşağıdaki formülle verilir:

\[y=f(x)+\varepsilon\]

Burada, $\varepsilon$, $0$ ortalama ve $\sigma_{\varepsilon}$ standart sapma ile Normal dağılıma sahiptir, yani, $\varepsilon \sim N(0, \sigma_{\varepsilon})$.

$f(x)$, Vektör $x$’in sabit fakat bilinmeyen bir fonksiyonudur. Genel olarak, $y$’nin deterministik olmayan bir ilişkisi vardır. Aynı zamanda, $y$, $\varepsilon$’un $x$ kullanılarak tahmin edilemeyen bir fonksiyonudur ve sözel olarak, $\varepsilon$ indirgenemez hatadır (irreducible error). $\varepsilon$ öğesini, rastgele bir hata terimi olan, düşük etkili veya ölçülemeyen bir değişken olarak düşünebilirsiniz. Gauss gürültüsü (gaussian noise) ile eş anlamlıdır, bundan dolayı sıfır ortalamaya sahiptir. Yani,

\[\mathbb{E}(\varepsilon) = 0, \,\,\,\,\,\, \operatorname{Var}(\varepsilon) = \sigma_{\varepsilon}^{2}\]

Şimdi, altta yatan gerçek hayat problemini modellemeye çalıştığımızda, bunun anlamı, gerçek (henüz bizim için bilinmeyen) $f$ fonksiyonuna yakın olacak şekilde bir $\hat{f}(x)$ fonksiyonunu bulmaya çalışmamızdır.

$\hat{f}(x)$ fonksiyonu, regresyon durumunda katsayılar, Destek Vektör Makineleri (SVM’ler) durumunda destek vektörleri ve dual katsayılar şeklinde olabilir ve eğitim verilerinden öğrenilir.

Eğitim verisini üreten temeldeki dağılım fonksiyonu (the underlying distribution generating training data), test (görünmeyen) veri üreten temeldeki dağılım fonksiyonuna (the underlying distribution generating test (unseen) data) ne kadar yakınsa, $\hat{f}(x)$ fonksiyonuyla temsil edilen model, görünmeyen verilere o kadar iyi genelleyecektir (generalization). Fonksiyon $\hat{f}(x)$, amacı eğitim verilerinin tahminlerini gözlemlenen değerlere (observed values) mümkün olduğunca yaklaştırmak olan bir kayıp fonksiyonunu en aza indirerek öğrenilir: $y \approx \hat{f}(x)$.

Ortalama kare hatası (kısaltma için MSE), bir $\hat{f}(x)$ tahmininin gerçek değer $y$ ile arasındaki farklarının karesinin ortalamasıdır ve şu şekilde tanımlanır:

\[\operatorname{MSE}=\mathbb{E}\left[(y-\hat{f}(x))^{2}\right]\]

Yan, önceden görülmemiş belirli bir test noktası $x$ için ortalama tahmin değerinin (eğitim verilerinin farklı gerçekleşmeleri (realization) üzerinden) temeldeki gerçek $f(x)$ fonksiyonuna olan farkı olarak tanımlanır.

\[\operatorname{bias}[\hat{f}(x)]=\mathbb{E}[\hat{f}(x)]-f(x)\]

“Eğitim verilerinin farklı gerçekleşmeleri” ile ne demek istediğimizi açıklamak için biraz zaman harcayalım. Belirli bir mahallede aile gelir düzeyi ile ev satış fiyatları arasındaki ilişkiyi izlemek istediğimizi varsayalım. Her haneden veriye ulaşabilseydik, çok doğru bir model eğitebilirdik. Ancak veri elde etmek maliyetli, zaman alıcı veya mahremiyet endişelerine tabi olabileceğinden, çoğu zaman temel kitlenin tüm verilerine erişimimiz olmaz. Bir gerçekleşme, eğitim verilerimiz olarak temel alınan verilerin yalnızca bir kısmına erişimimiz olduğu anlamına gelir.Bu gerçekleşme, üzerinde çalıştığımız kitleyi iyi temsil etmeyebilir (örneğin, yalnızca belirli bir eğitim düzeyine sahip olduğu hanelerin bulunduğu evlerde anket yaparsak) veya kitleyi iyi bir şekilde temsil edebiliriz (ırksal, eğitimsel, yaş veya diğer farklı yanlılıklar gerçekleşmeden). Dolayısıyla, $\mathbb{E}[\hat{f}(x)]$ beklenen değerinin eğitim verilerinin farklı gerçekleşmeleri üzerinde olduğunu söylediğimizde, bu, temel kitleden bir örneklem çektiğimiz, modelimizi bu örneklem üzerinde eğittiğimiz, $\hat{f}(x)$’i hesapladığımız ve bu süreci birden çok kez tekrarladığımız (her seferinde farklı bir eğitim verisi ile) anlamına gelir. Tahminlerin ortalaması $\mathbb{E}[\hat{f}(x)]$’i temsil edecektir. Burada $\hat{f}(x)$, $x$ sabit olsa bile değişir, çünkü $\hat{f}$ eğitim verilerine bağlıdır. Dolayısıyla, $\hat{f}$, eğitim verilerinin farklı gerçekleşmeleri için farklı olacaktır. Daha matematiksel olarak, $\hat{f}$, eğitim verilerinde içerisinde bulunan rastgelelikten etkilenen bir rastgele değişkendir.

Varyans, eğitim verilerinin farklı gerçekleşmeleri için, $\hat{f}(x)$’in, beklenen değeri $\mathbb{E}[\hat{f}(x)]$’den ortalama kare sapması olarak tanımlanır.

\[\operatorname{Var}(\hat{f}(x))=\mathbb{E}\left[(\hat{f}(x)-\mathbb{E}[\hat{f}(x)])^{2}\right]\]

Ortalama Kare Hatasını (MSE’yi), yan, varyans ve indirgenemez hataya bağlayan formül ise şu şekildedir:

\[\operatorname{MSE}=\mathbb{E}\left[(y-\hat{f}(x))^{2}\right]= \left( \mathbb{E} \left[ \hat{f}(x) \right] − f(x) \right)^{2} + \mathbb{E} \left[ \left( \hat{f}(x) − \mathbb{E} \left[ \hat{f}(x) \right] \right)^{2} \right] + \sigma_{\varepsilon}^{2}\]

Sağ taraftaki üç terim de negatif değildir ve indirgenemez hata model seçiminden etkilenmez. Bu, test kümesi üzerinden elde edilen MSE değerinin, $\sigma_{\varepsilon}^{2}$’nin altına düşemeyeceği anlamına gelir.

Kolaylıkla anlaşılacağı üzere nokta tahmini (point estimation) için elde edilen yan-varyans ilişkisi, fonksiyon tahmini (function estimation) ile de elde edilmiştir.

Bu nedenle, bir makine öğrenimi algoritmasında, yan-varyans ayrıştırması (bias-variance decomposition), bir öğrenme algoritmasının belirli bir probleme göre beklenen genelleme hatasını (expected generalization error) üç terimin, yani, yanın, varyansın ve problemin kendisindeki gürültüden kaynaklanan, indirgenemez hata olarak adlandırılan bir niceliğin toplamı olarak analiz etmenin bir yoludur.

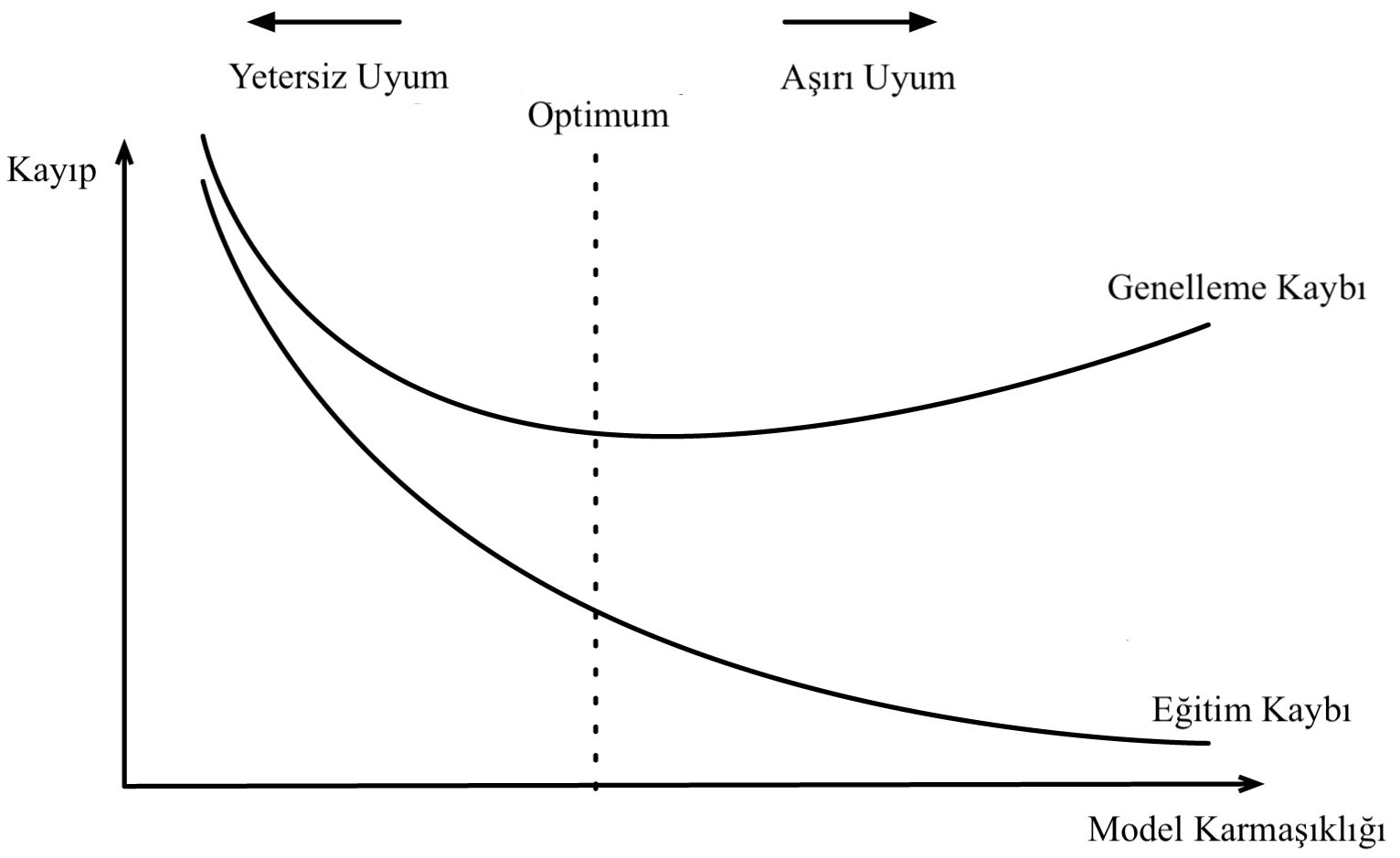
\[\text{Toplam Hata} = \text{Yan}^{2} + \text{Varyans} + \text{İndirgenemez Hata}\]

O halde, bir makine öğrenmesi modelini elde ederken, amacımız karesi alınmış bir yan, bir varyans ve bir sabit gürültü teriminin toplamına ayrıştırılan toplam hatayı en aza indirmektir. Daha sonra göreceğimiz gibi, yan ve varyans arasında bir denge vardır ve bu denge, Yetersiz Uyum (underfitting) ve Aşırı Uyum (overfitting) olarak adlandırılan iki kavrama yol açmaktadır. Özetle, Yetersiz Uyum, model eğitim veri kümesinde yeterince düşük bir hata değeri elde edemediğinde meydana gelir. Eğitim hatası ile test hatası arasındaki fark çok büyük olduğunda ise aşırı uyum meydana gelir. Bir modelin kapasitesini değiştirerek, bu modelin elimizdeki veri kümesine aşırı mı yoksa yetersiz mi uyum sağlayacağını kontrol edebiliriz.

Yan-Varyans Ayrışması’nın Kanıtı

Yukarıda verilen Yan-Varyan Ayrışması’nın (bias-variance decomposition) kanıtı oldukça kolaylık.

\[\begin{aligned} \operatorname{MSE}=\mathbb{E}\left[(y-\hat{f}(x))^{2}\right] &=\mathbb{E}\left[(f(x)+\epsilon-\hat{f}(x))^{2}\right] \,\,\,\,\,\,\,\,\,\,\, (1)\\ &=\mathbb{E}\left[(f(x)-\hat{f}(x))^{2}\right]+\mathbb{E}\left[\epsilon^{2}\right]+2 \mathbb{E}[(f(x)-\hat{f}(x)) \epsilon] \\ &=\mathbb{E}\left[(f(x)-\hat{f}(x))^{2}\right]+\underbrace{\mathbb{E}\left[\epsilon^{2}\right]}_{=\sigma_{\epsilon}^{2}}+2 \mathbb{E}[(f(x)-\hat{f}(x))] \underbrace{\mathbb{E}[\epsilon]}_{=0} \,\,\,\,\,\,\,\,\,\,\, (2)\\ &=\mathbb{E}\left[(f(x)-\hat{f}(x))^{2}\right]+\sigma_{\epsilon}^{2} \,\,\,\,\,\,\,\,\,\,\, (3) \end{aligned}\]

Burada, (1)’i yazabilmemizin sebebi $y=f(x)+\varepsilon$ olmasıdır. (2) ise kare açılımından, beklenen değerin doğrusallık özelliğinden, ve $\hat{f}(x)$ ve $\varepsilon$ rastlantı değişkenlerinin bağımsızlık özelliğinden yazılabilmektedir. İki rastgele değişken bağımsız olduğunda, bu rastlantı değişkenlerin çarpımlarının beklenen değerinin, ayrı ayrı beklenen değerlerinin çarpımına eşit olduğunu hatırlayın (yani $E(X Y) = E(X) E(Y)$). (3) numaralı eşitlikte ise, MSE’nin indirgenemez hata $\sigma_{\varepsilon}^{2}$ ve $\mathbb{E}\left[(f(x)-\hat{f}(x))^{2}\right]$’ye nasıl ayrıştığını görüyoruz. Şimdi, eşitliğin sağ tarafında ilk terimin nasıl daha fazla analiz edilebileceğini görelim.

\[\begin{aligned} \mathbb{E}\left[(f(x)-\hat{f}(x))^{2}\right]=& \mathbb{E}\left[((f(x)-\mathbb{E}[\hat{f}(x)])-(\hat{f}(x)-\mathbb{E}[\hat{f}(x)]))^{2}\right] \,\,\,\,\,\,\,\,\,\,\, (4)\\ =& \mathbb{E}\left[(\mathbb{E}[\hat{f}(x)]-f(x))^{2}\right]+\mathbb{E}\left[(\hat{f}(x)-\mathbb{E}[\hat{f}(x)])^{2}\right] -2 \mathbb{E}[(f(x)-\mathbb{E}[\hat{f}(x)])(\hat{f}(x)-\mathbb{E}[\hat{f}(x)])] \,\,\,\,\,\,\,\,\,\,\, (5)\\ =&(\underbrace{\mathbb{E}[\hat{f}(x)]-f(x)}_{=\operatorname{bias}[\hat{f}(x)]})^{2}+\underbrace{\mathbb{E}\left[(\hat{f}(x)-\mathbb{E}[\hat{f}(x)])^{2}\right]}_{=\operatorname{var}(\hat{f}(x))} - 2(f(x)-\mathbb{E}[\hat{f}(x)]) \mathbb{E}[(\hat{f}(x)-\mathbb{E}[\hat{f}(x)])] \,\,\,\,\,\,\,\,\,\,\, (6)\\ =& \operatorname{bias}[\hat{f}(x)]^{2}+\operatorname{Var}(\hat{f}(x)) -2(f(x)-\mathbb{E}[\hat{f}(x)])(\mathbb{E}[\hat{f}(x)]-\mathbb{E}[\hat{f}(x)]) \,\,\,\,\,\,\,\,\,\,\, (7)\\ =& \operatorname{bias}[\hat{f}(x)]^{2}+\operatorname{Var}(\hat{f}(x)) \end{aligned}\]

Eşitlik (4)’te, parantezin içine $\mathbb{E}[\hat{f}(x)]$ ekliyoruz ve içerisinden $\mathbb{E}[\hat{f}(x)]$ çıkartıyoruz ve Eşitlik (5)’te karenin içerisindeki terimleri genişletiriz. $\mathbb{E}[\hat{f}(x)]-f(x)$ bir sabittir çünkü hem $\mathbb{E}[\hat{f}(x)]$ hem de $f(x)$ sabittir. Bu nedenle, yan değerinin karesine beklenen değer (yani $(\mathbb{E}[\hat{f}(x)]-f(x))^{2}$) uygulamanın herhangi bir etkisi yoktur. Diğer bir deyişle, $\mathbb{E}\left[(\mathbb{E}[\hat{f}(x)]-f(x))^{2}\right] = (\mathbb{E}[\hat{f}(x)]-f(x))^{2}$’dir. Eşitlik (6)’da, $f(x)-\mathbb{E}[\hat{f}(x)]$ terimini beklenen değerden çıkartabiliyoruz çünkü dediğimiz gibi bu terim bir sabittir. Son olarak Eşitlik (7), beklenen değerin doğrusallık özelliği nedeniyle geçerlidir. Sonuç olarak, Eşitlik (8)’de $\mathbb{E}\left[(f(x)-\hat{f}(x))^{2}\right]$’nin yanın karesinin ve varyansın toplamı olduğunu görebiliyoruz. Eşitlik (3) ve (8)’i birleştirdiğimizde,

\[\mathbb{E}\left[(y-\hat{f}(x))^{2}\right]=\operatorname{bias}[\hat{f}(x)]^{2}+\operatorname{Var}(\hat{f}(x))+\sigma_{\epsilon}^{2}\]

denklemini elde ederiz.

Aşırı Uyum ve Yetersiz Uyum

Bir modelin kapasitesi, çok çeşitli fonksiyonlara uyum sağlama yeteneğidir (bir modelin kapasitesini değiştirmenin birçok yolu vardır). Model kapasitesi (model capacity), konsept olarak model karmaşıklığına (model complexity) çok yakındır (eş anlamlı değilse bile). Model kapasitesi, bir modelin ne kadar karmaşık bir örüntüyü veya ilişkiyi ifade edebileceği hakkında konuşmanın bir yoludur. Bir modelin kapasitesini tahmin etmenin en yaygın yolu, o modelin parametre sayısını saymaktır. Ne kadar fazla parametre olursa, genel olarak kapasite o kadar yüksek olacaktır. Tabii ki, bazen daha küçük bir ağ, daha karmaşık verileri daha büyük bir ağdan daha iyi modellemeyi öğrenebilir, bu nedenle, parametre sayısı, model kapasitesini ölçmek için mükemmel bir ölçüt olmaktan uzaktır.

Yüksek kapasiteli modeller genellikle düşük yan ve yüksek varyansa sahip çok esnek modellerdir. Böylelikle, eğitim veri kümesinin özelliklerini ezberleyerek, test kümesinde çok iyi çalışmazlar, böylelikle aşırı uyuma neden olurlar. Nispeten düşük kapasiteli modeller, yüksek yana ve düşük varyansa sahip rijit modellerdir. Yetersiz kapasiteye sahip modeller karmaşık görevleri çözemezler. Optimal tahmin yeteneğine sahip (yani yeteri biçimde karmaşık) bir model, elimizdeki görevin gerçek karmaşıklığı için uygundur ve yan ile varyans arasında en iyi dengeyi sağlayan modeldir.

Hem yüksek hem de düşük yan ve varyans kombinasyonlarını temsil eden bir boğa-gözü diyagramı (bull-eye diagram) kullanarak yan ve varyansın grafiksel bir görselleştirmesini oluşturabiliriz.

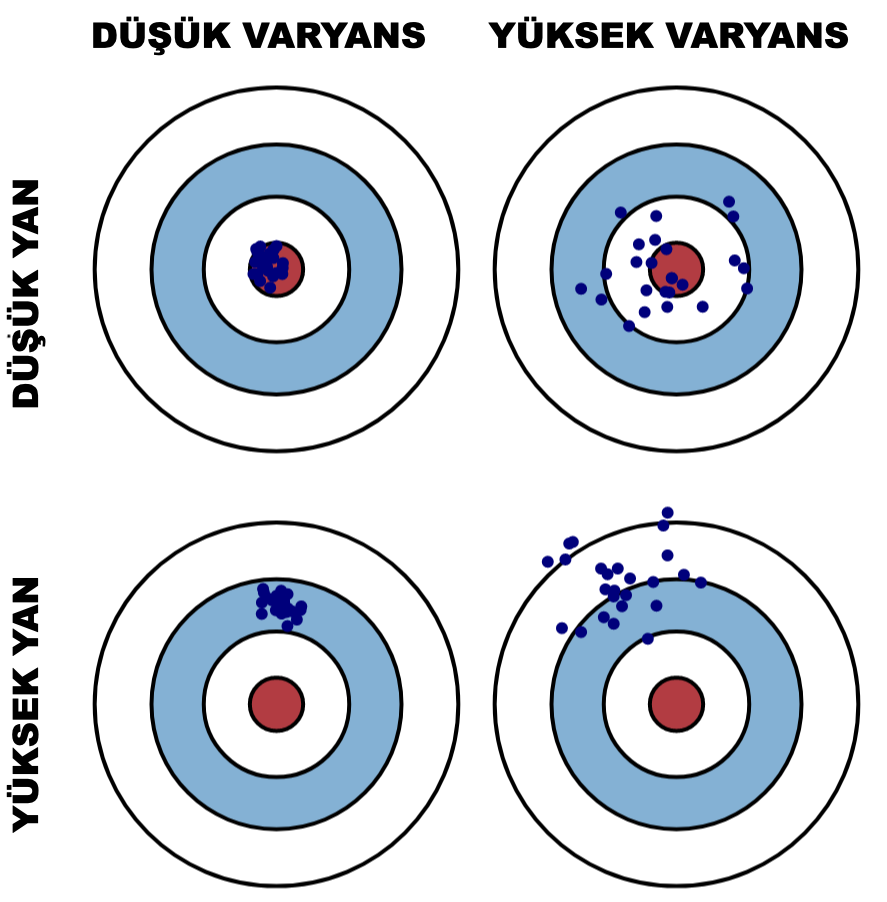
Yukarıda bir tahmin edici için elde ettiğimiz benzer grafiği burada basitçe elde edebiliriz:

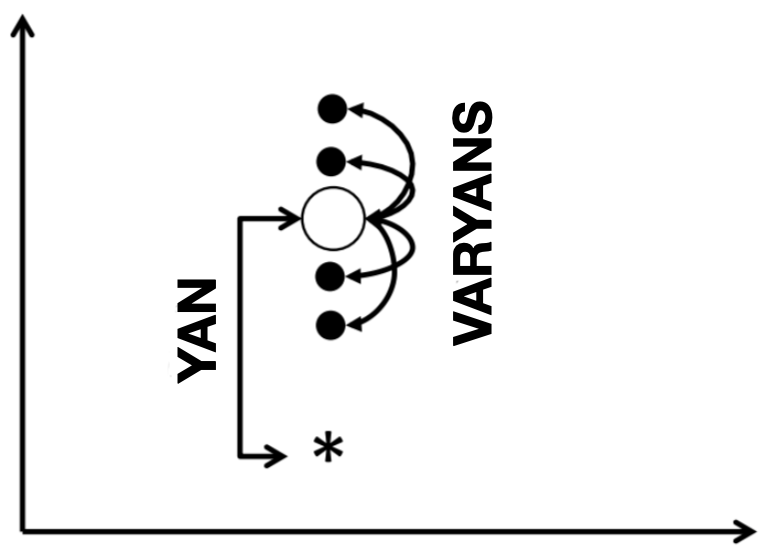
Yandan kaynaklanan hata, modelimizin beklenen (veya ortalama) tahmini ile tahmin etmeye çalıştığımız doğru değer arasındaki fark olarak alınır (bakınız bir tahmin edicinin yanı). Tabii ki sadece bir modeliniz var, bu yüzden beklenen veya ortalama tahmin değerlerinden bahsetmek biraz garip görünebilir. Bununla birlikte, tüm model oluşturma sürecini bir kereden fazla tekrarlayabileceğinizi hayal edin: her seferinde, yeni bir veri topluyorsunuz ve yeni bir model oluşturarak yeni bir analiz çalıştırıyorsunuz. Elde edilen veri kümelerindeki rastgelelik nedeniyle, ortaya çıkan modeller farklı tahminlere sahip olacaktır. Yan, genel olarak bu modellerin tahminlerinin doğru değerden ne kadar uzak olduğunu ölçer.

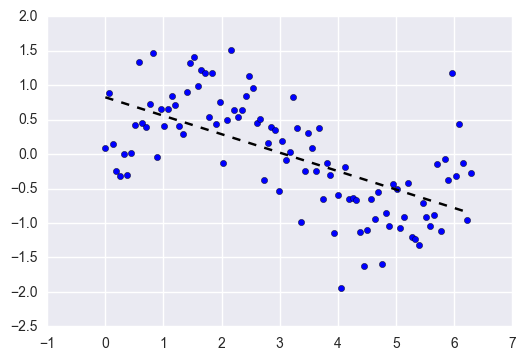
Yandan kaynaklanan hata, daha iyi tahminler yapmasına izin verebilecek verilerdeki sinyali öğrenemeyen bir tahminciden (estimator) gelen bir hatayı ifade eder. Genelleme hatasının bu kısmı, aslında ikinci dereceden (quadratic) olan verileri doğrusal olarak varsaymak gibi yanlış varsayımlardan kaynaklanmaktadır. Yüksek yanlı bir model, büyük olasılıkla eğitim verilerine yetersiz kalacaktır. Yetersiz uyumun birkaç nedeni olabilir, bunlardan en önemlileri: (1) modeliniz veriler için çok basit (örneğin, doğrusal bir model çoğu zaman yetersiz kalabilir), (2) sahip olduğunuz veya oluşturduğunuz değişkenler (öznitelikler) yeterince bilgilendirici değil. Yetersiz uyum sorununun çözümü, daha karmaşık bir model (ya daha fazla katman/ağaç veya farklı mimari yoluyla) denemek veya değişkenleri daha yüksek tahmin gücüne sahip olacak şekilde oluşturmaktır. Esnek olmayan bir modelin yüksek bir yana sahip olduğu söylenir çünkü eğitim verileri hakkında varsayımlarda bulunur. Örneğin, doğrusal bir sınıflandırıcı, verilerin doğrusal olduğu ve doğrusal olmayan ilişkilere uyması için yeterli esnekliğe sahip olmadığı varsayımında bulunur. Esnek olmayan bir model, eğitim verisine uyum sağlamak için yeterli kapasiteye sahip olmayabilir (veriden sinyali öğrenemez) ve model yeni bir veriye iyi genelleme yapamaz.

• Düşük yanlı Makine Öğrenmesi algoritmalarına örnekler: Karar Ağaçları, k-En Yakın Komşular Algoritması, Destek Vektör Makineleri vb…
• Yüksek yanlı ML algoritmalarına örnekler: Genel olarak, parametrik modeller yüksek yana sahiptir, bu da, bu modeller ile öğrenme sürecini hızlandırır ve modellerin anlaşılmasını kolaylaştırır, ancak genellikle daha az esnek hale getirir. Buna karşılık, algoritma yanlılığının sağladığını basit varsayımları karşılayamayan karmaşık problemler üzerinde daha düşük tahmin performansına sahiptirler. Doğrusal Regresyon, Naive Bayes algoritması, Doğrusal Diskriminant Analizi, Lojistik Regresyon vb…

Varyanstan kaynaklanan hata, belirli bir veri noktası için bir model tahmininin değişkenliği olarak anlaşılabilir. Bir daha tekrarlayacak olursak, tüm model oluşturma sürecini birden çok kez tekrarlayabileceğinizi hayal ediniz. Varyans, belirli bir nokta için tahminlerin modelin farklı gerçekleşmeleri arasında ne kadar değiştiğidir.

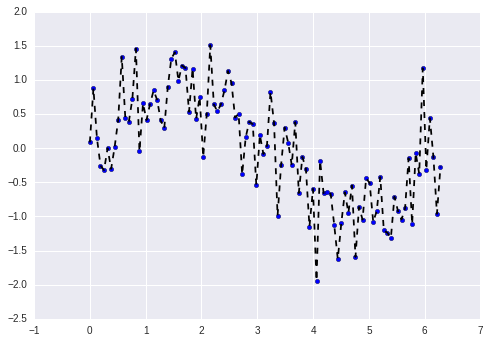
Varyanstan kaynaklanan hata, bir tahmincinin çok spesifik olmasından kaynaklıdır. Bu tür bir tahminci, sadece eğitim kümesine özgü ilişkileri öğrenir ancak yeni gözlemlere iyi bir şekilde genelleyemeyecektir. Eğitim kümesine özgü olan ancak yeni gözlemlere de iyi bir şekilde genellemeyen öğrenme ilişkileri nedeniyle oluşan bir hatayı ifade eder. Bu hata türü, modelin eğitim verilerindeki küçük varyansyonlara aşırı duyarlılığından kaynaklanmaktadır.

Yüksek serbestlik derecesine sahip bir model (yüksek dereceli bir polinom modeli gibi), yüksek varyansa sahip olacaktır ve dolayısıyla eğitim verilerini aşırı uyum sağlayacaktır. Bu tür bir model, yalnızca eğitim verilerindeki gerçek ilişkileri (sinyalleri) değil, aynı zamanda gürültüyü de öğrenecektir. Bu durum ise modelin yeni bir veri kümesi üzerindeki performansını olumsuz yönde etkileyecektir. Böylelikle aşırı uyum gerçekleşecektir. Bu, eğitim verilerindeki gürültü veya rastgele dalgalanmaların model tarafından kavram (konsept) olarak öğrenildiği anlamına gelir. Sorun, bu kavramların yeni verilere uygulanamaması ve modelin genelleme yeteneğini olumsuz etkilemesidir.

Aşırı uyum, eğitim verilerine fazla uyum sağlayarak verileri ezberleyen çok esnek bir modelimiz (yüksek kapasiteye sahip, yani verilerin dağılımını yakalama gücü daha fazla olan bir model) olduğunda meydana gelir. Esnek bir modelin yüksek bir varyansa sahip olduğu söylenir çünkü eğitim verileri değiştikçe öğrenilen parametreler önemli ölçüde değişecektir. Küçük varyans hatasına sahip olan modeller, eğitim kümesindeki birkaç örneği değiştirirseniz çok fazla değişmez. Varyansı yüksek modeller, eğitim kümesindeki küçük değişikliklerden bile etkilenebilir.

• Düşük varyanslı Makine Öğrenmesi algoritmalarına örnekler: Doğrusal Regresyon, Doğrusal Diskriminant Analizi, Lojistik Regresyon vb…
• Yüksek varyanslı Makine Öğrenmesi algoritmalarına örnekler: Genellikle, çok fazla esnekliğe sahip parametrik olmayan Makine Öğrenmesi algoritmaları, Karar Ağaçları, k-En Yakın Komşular algoritması, Destek Vektör Makineleri vb…

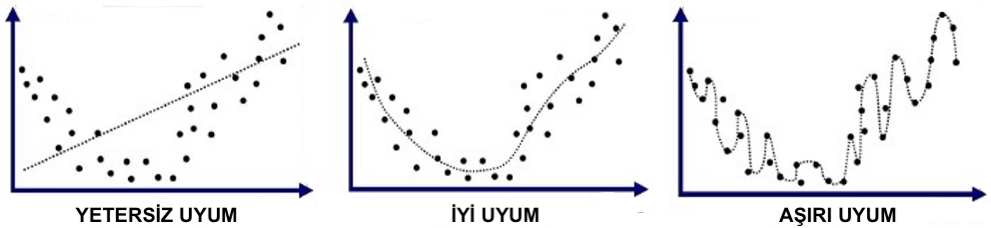
İndirgenemez hata, herhangi bir model ve bu model için yapılacak parametre seçimi ile azaltılamayan gerçek ilişkideki gürültü terimidir. Hatanın bu kısmını azaltmak için yapılan tek şey, verileri temizlemektir (örneğin, bozuk sensörler gibi veri kaynaklarını düzeltmek veya aykırı değerleri tespit etmek ve bu aykırı değerleri kaldırmak). Tahmine dayalı modellemede sinyal, veriden öğrenilmek istenen gerçek temel örüntü olarak düşünülebilir. Gürültü ise veri setindeki alakasız bilgileri veya rastgeleliği ifade eder.

Eğitim verilerini ezberleyen çok esnek (yüksek kapasiteli / karmaşık) bir model oluşturma ile eğitim verilerini öğrenemeyen esnek olmayan (düşük kapasiteli) bir model oluşturma arasındaki denge, yan-varyans ikilemi (bias-variance tradeoff) olarak bilinir ve Makine Öğrenmesinde temel bir kavramdır. Başka bir deyişle, varyansı azalttıkça yanı artırma eğilimindesinizdir. Yanı azalttıkça, varyansı artırma eğilimindesinizdir. Genel olarak amaç, yan ve varyans arasında bir denge olmasını sağlamak için dikkatli bir şekilde bir model seçmek ve bu modele ince ayar çekerek genel hatayı en aza indirgemektir. Bu model yeni bir veri üzerinde iyi bir tahminde bulunmak için yeterince genel, ancak mümkün olduğu kadar çok sinyal öğrenmek için yeterince spesifik olmalıdır. Doğru model ve onu kalibre etmek için sonsuz veri verildiğinde, hem yan hem de varyans terimlerini 0’a indirebilmeliyiz. Ancak, kusurlu modellerin ve sonlu verilerin olduğu bir dünyada durum böyle değildir.