Üretken Çekişmeli Ağlar (Generative Discriminative Networks - GANs) - 1. BÖLÜM

Bu blog yazısında, Üretken Çekişmeli Ağları (Generative Discriminative Networks - GANs) keşfedeceğiz. Bu tip ağları daha önce duymadıysanız, şimdiye kadar kaçırdığınız her şeyi öğrenme fırsatınız bu. Bu algoritma, Ian Goodfellow ve çalışma arkadaşları tarafından 2014 yılında literatüre tanıtılmıştır. 2014’ten beri var olmalarına rağmen GAN’lar, uygulamalardaki çok yönlülüğü ve veri üretmedeki olağanüstü sonuçlarıyla geniş çapta yıllardır kullanılmaktadır.

Peki neden GAN’lar kullanılmaktadır?

• Eğitim verileriniz yeterli değilse, hiç problem değil! GAN’lar verileriniz hakkında bilgi edinebilir ve veri kümenizi artıran sentetik görüntüler oluşturabilir.
• Verilen dağılımdan herhangi bir gerçek kişiye ait olmasa da, insan yüzlerinin fotoğraflarına benzeyen görüntüler oluşturabilir. Bu inanılmaz değil mi?
• Açıklamalardan görüntüler oluşturabilirsiniz (metinden görüntü sentezi).
• Bir videonun çözünürlüğünü iyileştirerek daha ince ayrıntıları yakalayabilirsiniz (düşük çözünürlükten yüksek çözünürlüğe).
• Ses alanında bile, GAN’lar sentetik, aslına uygun ses üretmek veya sesli çeviriler yapmak için kullanılabilir.

Hepsi bu değil. GAN’lar daha fazlasını yapabilir. Bugün bu kadar güçlü ve rağbet görmelerine şaşmamalı!

Üretken Çekişmeli Ağlar için Kayıp Fonksiyonu

Denetimli Öğrenmede (Supervised Learning), Üretken Modeller (Generative Model) ve Ayrımcı Modeller (Discriminative Model) olmak üzere iki farklı modelleme türü vardır. Ayrımcı Modeller, bir veri noktasının hangi sınıfa ait olduğunu tahmin etmek için modelin bir karar sınırını (decision boundary) öğrendiği Sınıflandırma görevini çözmek için kullanılır. Öte yandan, Üretken Modeller, eğitim verisinin olasılık dağılımıyla aynı olasılık dağılımını izleyen sentetik veri noktaları oluşturmak için kullanılır. Bu blog yazısının konusu olan Üretken Çekişmeli Ağlar (GAN’lar), Üretken Modeller olarak adlandırılan algoritmalar grubuna aittir.

GAN’lar, aynı anda eğitilmiş iki sinir ağından oluşan makine öğrenmesi yöntemlerinin bir sınıfıdır. GAN mimarisi, iki sinir ağı tarafından temsil edilen iki farklı aşamadan oluşmaktadır. Bu sinir ağlarından biri Üretici (generator), diğeri ise Ayrıştırıcı (discriminator) olarak adlandırılır. Üretici sahte veri üretmek için kullanılır. Ayrıştırıcı ise, kendisine verilen girdinin gerçek mi yoksa sahte mi olduğunu sınıflandırmak için kullanılır.

Görüntü üretimi (image generation) için kullanıldığında, Üretici sinir ağı, tipik olarak evrişimsiz bir sinir ağıdır (deconvolutional neural network). Ayrıştırıcı sinir ağı ise evrişimli bir sinir ağıdır (convolutional neural network).

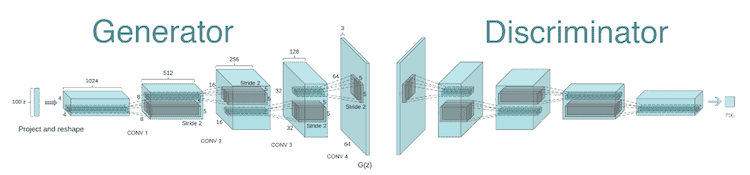
Buradaki temel düşünce, $\{x_{1}, x_{2}, \dots, x_{m} \}$ gibi gerçek verilerden oluşan bir veri kümesi verildiğinde, bu veri kümesindekilere benzer (similar) veriler elde etmektir. GAN’ların kullanım amacı ise, veri üretmek için kullanılacak Üretici sinir ağının, gerçek verilerden ayırt edilemez örnekler oluşturmasıdır. Matematiksel olarak, bu, rastgele değişkenlerin dağılımlarının eşit olması demektir. Bunu söylemenin başka bir yolu, bu rastlantı değişkenlerinin olasılık yoğunluk fonksiyonlarının eşit olmasıdır: $p_g(x)=p_{data}(x)$. Burada, $p_g$ üreticiden çıkan örneklerin olasılık fonksiyonunu ve $p_{data}$ ise gerçek verilerin olasılık fonksiyonunu temsil etmektedir. Bu tam olarak GAN’ın mantığını oluşturmaktadır. Yani, optimal üretici olan $G_{\theta_{g}}$’nin $p_g(x)=p_{data}(x)$’i sağladığı bir optimizasyon problemi bulmamız gerekmektedir.

Bu iki model birbiriyle sürekli etkileşim halindedir. Üretici, veriyi, Ayrıştırıcı’nın artık sahte olarak ayırt edemeyecek şekilde nasıl oluşturacağını öğrenmesi gerekir. Gerçekçi bir veri oluşturmayı başarana kadar Üretici’nin bilgilerini geliştiren durum bu iki ekip arasındaki rekabettir.

Sinir ağları modellemesi temelde iki şeyi tanımlamayı gerektirir: bir mimari ve bir kayıp fonksiyonu. Üretken Çekişmeli Ağların mimarisini zaten tanımlamıştık. İki farklı ağdan oluşur:

• İlk modele Üretici (Generator) denir ve beklenene benzer yeni veriler üretmeyi amaçlar. Üretici, sahte sanat eserleri yaratan bir insan sanatkarına benzetilebilir. $p_z$ yoğunluğuna sahip rastgele bir $z$ girdisi alan ve eğitimden sonra hedeflenen olasılık dağılımını takip etmesi gereken bir $x_g = G(z)$ çıktısı döndüren üretken bir ağ $G(\cdot)$’dır. Bu sinir ağını $G(z, \theta_{g})$ veya $G_{\theta_{g}} (z)$ ile gösterebiliriz. Burada, $\theta_{g}$, bu sinir ağını tanımlayan ağırlıkları veya parametreleri göstermektedir.
• İkinci model Ayrıştırıcı (Discriminator) olarak adlandırılmıştır. Bu modelin amacı, bir girdi verisinin “gerçek” olup olmadığını, yani, orijinal veri kümesine ait olup olmadığını, veya bir sahtekar tarafından oluşturulmuş “sahte” bir veri olup olmadığını tanımaktır. Bu senaryoda, Ayrıştırıcı, sanat eserlerinin “gerçek” veya “sahte” olduğunu tespit etmeye çalışan bir sanat uzmanına benzer. “Doğru (true)” (yoğunluğu $p_{data}$ olan bir $x_{data}$) veya “üretilmiş (generated)” (yani yoğunluğu $p_g$ olan bir $x_g$. Burada, $p_g$, $G(\cdot)$ ağından geçen $p_z$ yoğunluğundan oluşmaktadır.) bir $x$ girdisi alan ve $x$’in $D(x)$ olasılığını döndüren ayrıştırıcı bir ağ $D(\cdot)$’dır. Benzer şekilde, bu ikinci sinir ağı $D(x, \theta_{d})$ veya $D_{\theta_{d}} (x)$ ile gösterilir ve verilerin gerçek veri kümesinden gelme olasılığını $(0,1)$ aralığında verir (Tabii ki, olasılık değeri elde edebilmek için bu sinir ağının son katmanı olarak bir sigmoid fonksiyonu kullanılır). Burada, $\theta_{d}$, bu sinir ağını tanımlayan ağırlıkları veya parametreleri göstermektedir.

Sonuç olarak, Ayrıştırıcı, girdi verilerini gerçek veya sahte olarak doğru bir şekilde sınıflandırmak için eğitilir. Bu, herhangi bir gerçek veri girdisi $x$’in gerçek veri kümesine ait olarak sınıflandırılma olasılığını en üst düzeye çıkarırken (maximizing), herhangi bir sahte verinin gerçek veri kümesine ait olarak sınıflandırılma olasılığını en aza indirecek (minimizing) şekilde ağırlıklarının güncellendiği anlamına gelir. Daha teknik bir ifadeyle, kullanılan kayıp/hata fonksiyonu, $D_{\theta_{d}} (x)$ fonksiyonunu maksimize eder ve ayrıca $D_{\theta_{d}} \left( G_{\theta_{g}} (z) \right)$’yi minimize eder.

Ayrıca, Üretici mümkün olduğunca gerçekçi veriler üreterek Ayrıştırıcı’yı kandırmak üzere eğitilmiştir; bu, Üretici’nin ağırlıklarının (parametrelerinin), herhangi bir sahte verinin gerçek veri kümesine ait olarak sınıflandırılma olasılığını en üst düzeye çıkarmak (maximizing) için optimize edildiği anlamına gelir. Daha resmi bir ifadeyle, bu üretici ağ için kullanılan kayıp/hata fonksiyonunun, $D_{\theta_{d}} \left( G_{\theta_{g}} (z) \right)$’yi maksimize ettiği anlamına gelir.

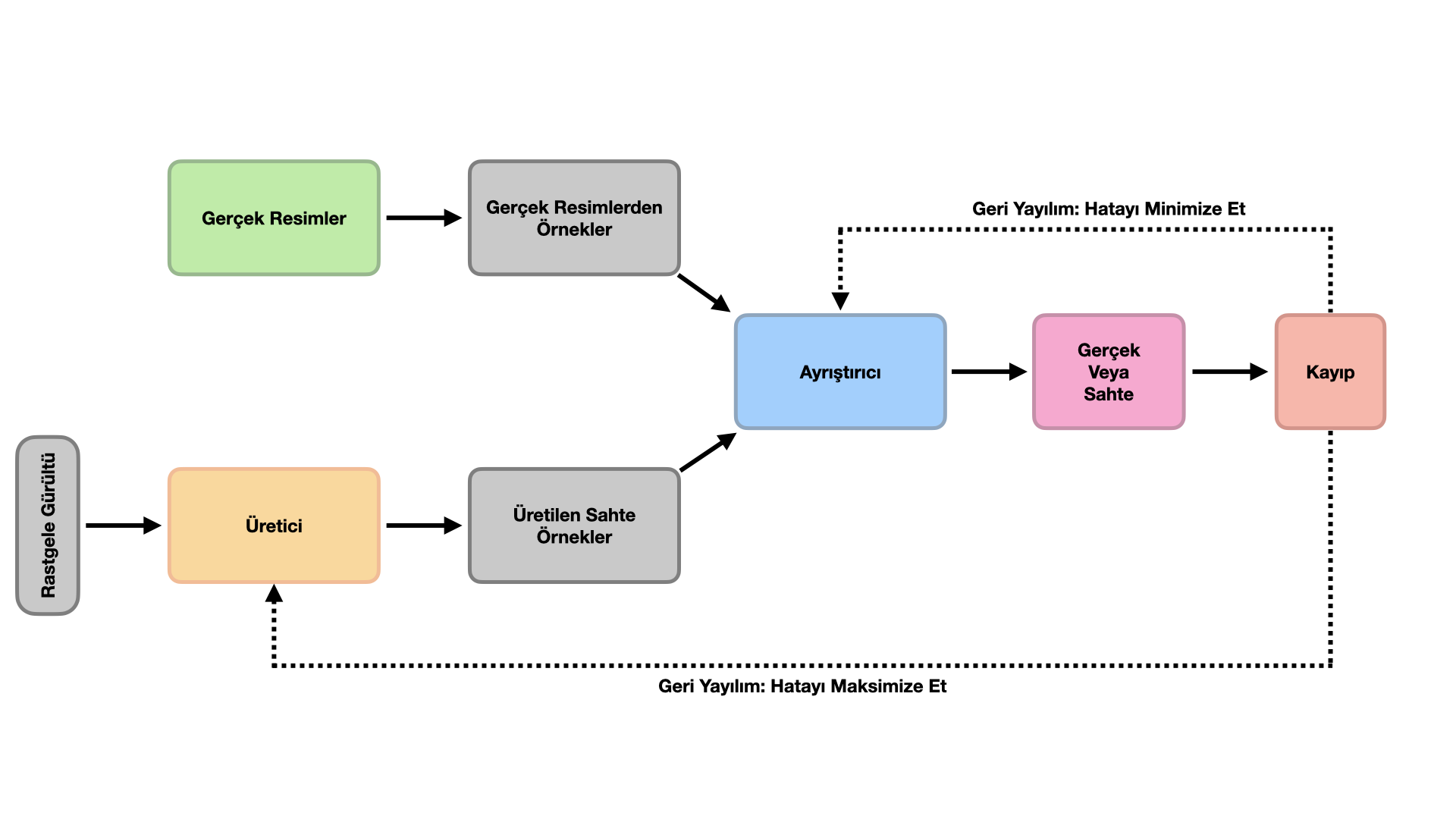
Adlarından da anlaşılacağı gibi, gerçek görünümlü görüntüler oluşturmak için bir üretici kullanılır ve ayrıştırıcının görevi hangi görüntünün sahte olduğunu belirlemektir. Biri (üretici) diğerini (ayrıştırıcı) kandırmaya çalışırken, diğeri (ayrıştırıcı) kandırılmamaya çalıştığı için bu iki sinir ağı sürekli savaş halindedir. En iyi görüntüleri oluşturmak için çok iyi bir üreticiye ve çok iyi bir ayrıştırıcıya ihtiyacınız vardır. Bunun nedeni, Üretici yeterince iyi değilse, Ayrıştırıcı’yı asla kandıramayacak ve model asla yakınsamayacaktır. Ayrıştırıcı kötüyse, hiçbir anlamı olmayan görüntüler de gerçek olarak sınıflandırılacak ve bu nedenle modeliniz asla eğitilemeyecektir ve karşılığında asla istenen çıktıyı üretemeyeceksiniz.

Üretici, bir rastgele gürültü ile sahte bir veri oluşturur. Diğer bir deyişle, rastgele gürültü bir Gauss dağılımına sahip olabilir ve değerler bu dağılımdan örneklenebilir ve üretici ağına beslenebilir ve bir sahte görüntü oluşturulabilir. Oluşturulan bu görüntü, Ayrıştırıcı tarafından gerçek bir görüntü ile karşılaştırılır ve verilen görüntünün sahte mi gerçek mi olduğunu belirlenmeye çalışılır.

Yukarıdaki bilgiler ışığında, şimdi GAN’ların “teorik” kayıp fonksiyonuna daha yakından bakalım. GAN’lar bir olasılık dağılımını kopyalamaya çalışır. Bu nedenle, GAN’ın Üretici sinir ağı tarafından üretilen verilerin dağılımı ile gerçek verilerin dağılımı arasındaki mesafeyi yansıtan bir kayıp fonksiyonu kullanmalıyız.

Eğitim sırasında hem Ayrıştırıcı hem de Üretici zıt kayıp fonksiyonlarını optimize etmeye çalıştıklarından, $V(G_{\theta_{g}}, D_{\theta_{d}})$ değer fonksiyonuna (value function) sahip bu iki sinir ağı, bir “minimax” oyunu oynayan iki ajan olarak düşünülebilirler. Bu minimax oyununda, Üretici çıktılarının (yani sahte verinin) “gerçek” olarak tanınması olasılığını en üst düzeye çıkarmaya çalışırken, Ayrıştırıcı aynı değeri en aza indirmeye çalışmaktadır:

\[\min_{\theta_{g}} \max_{\theta_{d}}\,\, V(G_{\theta_{g}}, D_{\theta_{d}}) = E_{x \sim p_{data}} \left[ \log \left( \underbrace{D_{\theta_{d}} (x)}_{\text{gerçek veri $x$ için Ayrıştırıcı'nın çıktısı}} \right) \right] + E_{z \sim p_{z}} \left[ \log \left( 1 - \underbrace{D_{\theta_{d}} \left( G_{\theta_{g}}(z)\right)}_{\text{üretilmiş sahte veri $G_{\theta_{g}} (z)$ için Ayrıştırıcı'nın çıktısı}} \right) \right]\]

Bu fonksiyonda,

• $D_{\theta_{d}} (x)$, gerçek veri $x$’in “gerçek” olarak sınıflandırma olasılığının Ayrıştırıcı tarafından yapılan bir kestirimidir.
• $E_{x \sim p_{data}}$, tüm gerçek veri örnekleri üzerinden beklenen değerdir.
• $G_{\theta_{g}}(z)$, $z$ gürültüsü verildiğinde Üretici’nin çıktısıdır.
• $D_{\theta_{d}} \left( G_{\theta_{g}}(z)\right)$, sahte (Üretici tarafından üretilmiş) bir örneğin “gerçek” olarak sınıflandırma olasılığının Ayrıştırıcı tarafından yapılan bir kestirimidir.
• $E_{z \sim p_{z}} $, Üretici tarafından üretilen tüm rastgele girdiler üzerinden beklenen değerdir (aslında, üretilen tüm sahte örnekler $G_{\theta_{g}}(z)$ üzerinden beklenen değerdir).
• Bu formül, gerçek verilerin dağılımı ve üretilen verilerin dağılımı arasındaki çapraz entropiden türetilir.
• Bu kayıp fonksiyonuna aynı zamanda, Minimax loss kaybı (Minimax loss) denilmektedir.

Formülü yorumlamak oldukça kolaydır. Ayrıştırıcı ($\theta_{d}$ parametreli bir sinir ağı), $D_{\theta_{d}} (x)$ olasılığı 1’e (gerçek) ve $D_{\theta_{d}} \left( G_{\theta_{g}}(z)\right)$ olasılığı 0’a (sahte) yakın olacak şekilde bu amaç fonksiyonunu maksimize etmek istemektedir. Üretici ($\theta_{g}$ parametreli bir sinir ağı) $D_{\theta_{d}} \left( G_{\theta_{g}}(z)\right)$ olasılığı 1’e yakın olacak şekilde bu amaç fonksiyonunu minimize etmek istemektedir (Ayrıştırıcı, üretici tarafından üretilen $G_{\theta_{g}}(z)$’nin gerçek olduğunu düşünerek kandırılmaktadır).

Ayrıştırıcı, amaç fonksiyonunu maksimize etmeye çalışır, bu nedenle amaç fonksiyonu üzerinde gradyan çıkış (gradient ascent) algoritmasını gerçekleştirebiliriz. Benzer şekilde, Üretici amaç fonksiyonunu minimize etmeye çalışır, bu nedenle amaç fonksiyonu üzerinde gradyan inişi (gradient descent) algoritmasını gerçekleştirebiliriz. Gradyan iniş ve çıkış algoritmaları arasında geçiş yaparak Üretken Çekişmeli Ağlar eğitilebilir:

1. Ayrıştırıcıda gradyan çıkış algoritması:

\[\max_{\theta_{d}}\,\, E_{x \sim p_{data}} \left[ \log \left( D_{\theta_{d}} (x) \right) \right] + E_{z \sim p_{z}} \left[ \log \left(1 - D_{\theta_{d}} \left( G_{\theta_{g}}(z)\right) \right) \right]\]

1. Üreticide gradyan iniş algoritması:

\[\min_{\theta_{g}}\,\, E_{z \sim p_{z}} \left[ \log \left(1 - D_{\theta_{d}} \left( G_{\theta_{g}}(z)\right) \right) \right]\]

Ancak uygulamada, Üretici için kullanılan amaç fonksiyonunu optimize etmenin çok iyi çalışmadığı gözlemlenmiştir. Üretici sinir ağı tarafından yeni bir örnek oluşturulduğunda, sahte olarak sınıflandırılması muhtemeldir. Ayrıştırıcı sinir ağı, gradyanları kullanarak bunu öğrenecektir ve böylelikle, Üretici sinir ağı daha da gelişecektir. Ancak, elde edilen gradyanların düz olduğu uygulamada görülmüştür. Gradyanların düzleşmesi, GAN modelinin öğrenmesini zorlaştırır. Bu nedenle, Üretici için kullanılan amaç fonksiyonu aşağıdaki gibi değiştirilir:

\[\max_{\theta_{g}}\,\, E_{z \sim p_{z}} \left[ \log \left( D_{\theta_{d}} \left( G_{\theta_{g}}(z)\right) \right) \right]\]

Böylelikle, Ayrıştırıcı’nın doğru olma olasılığını en aza indirmek yerine, Ayrıştırıcı’nın yanlış olma olasılığını en üst düzeye çıkarıyoruz. O halde, bu amaç fonksiyonuna göre Üretici üzerinde gradyan çıkışı algoritmasını gerçekleştirebiliriz.

Ancak, Üretken Çekişmeli Ağları eğitmek, diğer sinir ağlarını eğitmeye göre daha kararsız (unstable) bir sürece neden olur çünkü GAN modellerinde, tek bir geri yayılımdan iki ağı eğitmeniz gerekmektedir. Bu nedenle doğru amaç fonksiyonunu kullanmak büyük bir fark yaratmaktadır.

Ayrıca, GAN’ları eğitirken amacımızın minimum kayıp değeri (minimum loss value) aramak olmadığını, iki sinir ağı arasında bir miktar denge (equilibrium) bulmak olduğunu unutmayınız!

Çekişmeli kayıp fonksiyonunu sıfırdan türetme

Yukarıdaki kayıp fonksiyonunu kavramak zor olabilir ancak bu fonksiyonu elinizde sıfırdan elde etmeye çalıştığınızda, anlaşılması daha kolay olacaktır.

Kolaylıkla anlaşılacağı üzere, Ayrıştırıcı, ikili sınıflandırma (Binary classification - Real (Gerçek) veya Fake (Sahte)) gerçekleştiren bir sınıflandırıcıdan başka bir şey değildir. Peki, ikili sınıflandırma için hangi kayıp fonksiyonunu kullanıyoruz? İkili çapraz entropi (binary cross entropy) değil mi?

İkili çapraz entropi kaybı fonksiyonunun denklemi aşağıda verilmiştir:

\[L(\hat{y}, y) = y \cdot \log \left( \hat{y} \right) + (1-y) \log \left( 1-\hat{y} \right)\]

Burada, $\hat{y}$ model tarafından tahmin edilen etiket (label) ve $y$, gerçek etikettir (real label).

Ayrıştırıcı, ya gerçek bir görüntü olan $x$ ya da üretici tarafından üretilen $G_{\theta_{g}}(z)$ verisini alır. Ayrıştırıcı, bir ikili sınıflandırıcıdan başka bir şey olmadığı için, $D_{\theta_{d}} (x)$’i 1 (diğer bir deyişler, gerçek veri $x$, ayrıştırıcı tarafından “gerçek” olarak sınıflandırılır) ve $D_{\theta_{d}} \left( G_{\theta_{g}}(z)\right)$’yi 0 (diğer bir deyişle, Üretici tarafından üretilmiş sahte veri, Ayrıştırıcı tarafından “sahte” olarak sınıflandırılır) olarak etiketliyoruz. Ayrıştırıcı ağımızın, tüm $D_{\theta_{d}} (x)$’leri 1 ve tüm $D_{\theta_{d}} \left( G_{\theta_{g}}(z)\right)$’leri 0 olarak etiketlemesini istiyoruz. Doğru mu?

O halde, $x$ girdi olarak veirldiğinde, ayrıştırıcı tarafından tahmin edilen değeri $D_{\theta_{d}} (x)$ ve bu girdinin gerçek etiketi $1$’dir (gerçek görüntü, “gerçek” olarak sınıflandırılır). Bu durumda,

\[\begin{split} L \left( D_{\theta_{d}} (x), 1 \right) &= 1 \cdot \log \left( D_{\theta_{d}} (x) \right) + (1 - 1) \log \left( 1 - D_{\theta_{d}} (x) \right)\\ &= \log \left( D_{\theta_{d}} (x) \right) \end{split}\]

Ayrıştırıcı, $\log \left( D_{\theta_{d}} (x) \right)$ maksimize etmelidir ve $\log$ fonksiyonu, monotonik bir fonksiyon olduğundan, Ayrıştırıcı $D_{\theta_{d}} (x)$’i maksimize ederse $\log \left( D_{\theta_{d}} (x) \right)$ otomatik olarak maksimize edilecektir.

Öte yandan, girdi olarak $G_{\theta_{g}}(z)$ verildiğinde, bu girdinin Ayrıştırıcı sinir ağından geçtikten sonra tahmin edilen değeri $D_{\theta_{d}} \left( G_{\theta_{g}}(z)\right)$ olur. $G_{\theta_{g}}(z)$ girdisinin üretilen veri olduğunu ve sahte olduğunu, dolayısıyla gerçek etiketinin $0$ olduğunu unutmayın. O halde,

\[\begin{split} L \left( D_{\theta_{d}} \left( G_{\theta_{g}}(z)\right), 0 \right) &= 0 \cdot \log \left( D_{\theta_{d}} \left( G_{\theta_{g}}(z)\right) \right) + (1 - 0) \log \left( 1 -D_{\theta_{d}} \left( G_{\theta_{g}}(z)\right) \right)\\ &= \log \left( 1 - D_{\theta_{d}} \left( G_{\theta_{g}}(z)\right) \right) \end{split}\]

Ayrıştırıcı’nın $\log \left( 1 - D_{\theta_{d}} \left( G_{\theta_{g}}(z)\right) \right)$ değerini maksimize etmesi gerekir, bu da $D_{\theta_{d}} \left( G_{\theta_{g}}(z)\right)$’yi minimize etmesi gerektiği anlamına gelir. Yani, Üretici, Ayrıştırıcı’yı kandıramamaktadır.

Böylece, tek bir örnek için Ayrıştırıcı’nın kayıp fonksiyonu:

\[\text {Maksimize Et}\left[ \log \left( D_{\theta_{d}} (x) \right) + \log \left( 1 - D_{\theta_{d}} \left( G_{\theta_{g}}(z)\right) \right) \right]\]

Sözel olarak söyleyecek olursak, Ayrıştırıcı, yukarıdaki kayıp fonksiyonunu genel olarak maksimize etmek için $D_{\theta_{d}} (x)$’i maksimize edecek ve $D_{\theta_{d}} \left( G_{\theta_{g}}(z)\right)$’yi minimize edecektir. $D_{\theta_{d}} (x)$ ve $D_{\theta_{d}} \left( G_{\theta_{g}}(z)\right)$’nin her ikisinin de olasılık değerleri olduğuna ve her ikisinin de 0 ile 1 arasında yer aldığına dikkat ediniz.

Şimdi, bir yığın (batch) için ayrıştırıcının kayıp fonksiyonu,

\[\text {Maksimize Et}\,\, \left[ E_{x \sim p_{data}} \left[ \log \left( D_{\theta_{d}} (x) \right) \right] + E_{z \sim p_{z}} \left[ \log \left(1 - D_{\theta_{d}} \left( G_{\theta_{g}}(z)\right) \right) \right] \right]\]

Burada, $p_{data}$, gerçek eğitim verilerinin olasılık dağılımıdır ve $p_{z}$, gürültü vektörü $z$’nin olasılık dağılımıdır. Tipik olarak, $p_{z}$ Gauss dağımına veya Uniform dağılıma sahiptir.

Sözel olarak ifade edilirse, hem eğitim örneklerine (yani gerçek veri kümesine) hem de Üretici’den gelen örneklere (yani sahte veri kümesine) doğru etiketi atama olasılığını en üst düzeye çıkarmak için Ayrıştırıcı’yi eğitiriz. Ayrıştırıcı için bulunan kayıp fonksiyonu doğrudan uygulanırsa, stokastik iniş (stochastic descent) yerine stokastik çıkış (stochastic ascend) kullanılarak model ağırlıklarında değişiklikler yapılmasını gerektirecektir.

Şimdi Üretici’nin amaç fonksiyonunu bulalım.

Üretici’nin mümkün olduğunca gerçek görüntüler üreterek Ayrıştırıcı’yı kandırması gerekmektedir. Yani, Üretici öyle bir $G_{\theta_{g}}(z)$ üretmeli ki, bu veri Ayrıştırıcı’dan geçtikten sonra, $1$ (yani “gerçek”) olarak tahmin edilmelidir (etiketlenmelidir.)

ancak Ayrıştırıcı’nın tüm $D_{\theta_{d}} \left( G_{\theta_{g}}(z)\right)$’leri 0 olarak etiketlemesini istiyoruz. İkili çapraz entropi kullanılarak bu durum şöyle yazılabilir:

\[L \left( D_{\theta_{d}} \left( G_{\theta_{g}}(z)\right), 0 \right) = \log \left( 1 - D_{\theta_{d}} \left( G_{\theta_{g}}(z)\right) \right)\]

Yukarıdaki sadece bir örnek içindir. Bir yığın üzerinde gerçekleşecek kayıp:

\[L \left( D_{\theta_{d}} \left( G_{\theta_{g}}(z)\right), 0 \right) = E_{z \sim p_{z}} \left[ \log \left( 1 - D_{\theta_{d}} \left( G_{\theta_{g}}(z)\right) \right) \right]\]

şeklindedir. Ayrıştırıcı’nın yukarıdaki kayıp fonksiyonunu maksimize etmek istediğinden bahsetmiştik. Üretici, Ayrıştırıcı’yı kandırmak istediği için yukarıdaki kayıp fonksiyonunu minimize etmek isteyecektir. Başka bir deyişle, Üretici, Ayrıştırıcı’nın sahte üretilen verileri gerçek olarak etiketlemesini istemektedir. Şimdi, Ayrıştırıcı’nın $ D_{\theta_{d}} \left( G_{\theta_{g}}(z)\right)$’yi minimize etmek istediği ve Üretici’nin $D_{\theta_{d}} \left( G_{\theta_{g}}(z)\right)$’yi maksimize etmek istediği çok açıktır.

Üretici’nin hiçbir zaman gerçek bir veri (real data) görmeyeceğini unutmayın, ancak eksiksiz olması için Üretici için kayıp fonksiyonu aşağıdaki gibi yazılabilir!

\[\text {Minimize Et}\,\, \left[ E_{x \sim p_{data}} \left[ \log \left( D_{\theta_{d}} (x) \right) \right] + E_{z \sim p_{z}} \left[ \log \left(1 - D_{\theta_{d}} \left( G_{\theta_{g}}(z)\right) \right) \right] \right]\]

Üretici’nin ilk terim üzerinde hiçbir kontrolü olmadığını, bu nedenle yalnızca ikinci terimi minimize edeceğini unutmayınız.

$\theta_{d}$’nin Ayrıştırıcı sinir ağının parametreleri olduğunu ve $\theta_{g}$’nin Üretici sinir ağının parametreleri olduğunu varsayalım. Böylece kayıp fonksiyonunu şu şekilde yazabiliriz:

\[\min_{\theta_{g}} \max_{\theta_{d}}\,\, E_{x \sim p_{data}} \left[ \log \left( D_{\theta_{d}} (x) \right) \right] + E_{z \sim p_{z}} \left[ \log \left(1 - D_{\theta_{d}} \left( G_{\theta_{g}}(z)\right) \right) \right]\]

GAN kayıp fonksiyonunun optimal değeri

$V(G_{\theta_{g}}, D_{\theta_{d}}$ ifadesini açalım. Ayrıştırıcının ($D_{\theta_{d}})$) bu fonksiyonu $\theta_{d}$ parametrelerine göre maksimize ettiğini biliyoruz. Burada, sabit bir $G_{\theta_{g}}$ üretici verildiğinde, Ayrıştırıcı ikili sınıflandırma gerçekleştirmektedir. Ayrıştırıcı, $x \sim p_{data}$ olasılık fonksiyonuna sahip eğitim kümesindeki veri noktalarına $1$ olasılığını atar (yani bu örnekler gerçektir), ve Üreticiden gelmiş $x \sim p_{g}$ olasılık fonksiyonuna sahip üretilmiş örneklere $0$ olasılığını atar (yani bu örnekler sahtedir). Bu durumda, optimal Ayrıştırıcı şu şekildedir:

\[D_{G}^{\star} (x) = \frac{p_{data}(x)}{p_{data}(x) + p_{g}(x)}\]

Öte yandan, Üretici ($G_{\theta_{g}}$) sabit bir $D_{\theta_{d}}$ ayrıştırıcısı için $V(G_{\theta_{g}}, D_{\theta_{d}})$ amaç fonksiyonunu minimize etmeye çalışır.

Yukarıda elde edilen optimal ayrıştırıcı olan $D_{G}^{\star} (x)$’i $V(G_{\theta_{g}}, D_{\theta_{d}})$ amaç fonksiyonuna yerleştirdiğimizde

\[2D_{\textrm{JSD}}[p_{data}, p_{g}] - \log 4\]

ifadesini elde ederiz. Burada, $D_{\textrm{JSD}}$ terimi, Kullback-Leibler ıraksaması’nın (Kullback-Leibler divergence) simetrik formu olarak da bilinen Jenson-Shannon ıraksaması’dır (Jenson-Shannon divergence) ve şu şekilde hesaplanır:

\[D_{\textrm{JSD}}[p, q] = \frac{1}{2} \left( D_{\textrm{KL}}\left[p, \frac{p+q}{2} \right] + D_{\textrm{KL}}\left[q, \frac{p+q}{2} \right] \right)\]

Jenson-Shannon ıraksaması, Kullback-Leibler ıraksaması’nın tüm özelliklerini karşılar ve ek avantajı vardır: $D_{\textrm{JSD}}[p,q] = D_{\textrm{JSD}}[q,p]$. Bu mesafe ölçütü (distance metric) ile, GAN amaç fonksiyonu için optimal Üretici $p_{data} = p_{g}$ olduğunda gerçekleşir, yani, veri üretme sürecini mükemmel bir şekilde kopyalayan bir üretken model vardır. Optimal üreticiler ($G^{\star} (\cdot)$) ve ayrıştırıcılar ($D_{G^{\star}}^{\star}(\mathbf{x})$) ile elde edebileceğimiz amaç fonksiyonunun optimal değeri $-\log 4$’tür.

Bir Üretken Çekişmeli Ağı Eğitmek

GAN modelinin yayınlandığı orijinal makaleye göre eğitim aşağıdaki şekilde gerçekleştirilir:

Özetle bir GAN’ı eğitmek için temel adımlar aşağıdaki gibi tanımlanabilir:

1. Her biri $m$ boyutunda olan bir gürültü kümesini ve bir gerçek veri kümesini örnekleyin.
2. Ayrıştırıcı sinir ağını bu veriler üzerinde eğitin.
3. $m$ boyutunda farklı bir gürültü alt kümesini örnekleyin.
4. Üretici sinir ağını bu veriler üzerinde eğitin.
5. Adım 1’den itibaren tekrarlayın.

Burada mini-yığın (mini-batch) stokastik gradyan iniş algoritması kullanılarak eğitim gerçekleştirilmiştir. Ayrıştırıcıya uygulanacak adımların sayısı olan $k$ bir hiper parametredir. Deneylerde hesaplama açısından en ucuz seçenek olan $k=1$ kullanılmıştır. Ancak bu $k$ hiperparametresi için en iyi bir değer yoktur.

Yukarıdaki algoritmadan, Üretici ve Ayrıştırıcı sinir ağlarının ayrı ayrı eğitildiği kolaylıkla fark edilebilir. Ayrıştırıcı sinir ağının eğitimi, gerçek verileri sahte olanlardan nasıl ayırt edeceğini bulmaya çalışırken, aynı zamanda Üreticinin kusurlarını nasıl fark edeceğini öğrenmelidir. Benzer şekilde, Üretici sini,r ağının eğitim aşamasında da Ayrıştırıcı’yı sabit tutarız. Aksi takdirde, Üretici sürekli hareket eden bir hedefi vurmaya çalışacak ve asla yakınsamayacaktır (converge).

Gradyan-tabanlı güncellemelerin herhangi bir standart gradyan-tabanlı öğrenme kuralını kullanabileceğini unutmayın. Orijinal çalışma için yapılan deneylerde Momentum yöntemi (https://ruder.io/optimizing-gradient-descent/) kullanılmıştır.

1. https://lilianweng.github.io/lil-log/2017/08/20/from-GAN-to-WGAN.html
2. https://srome.github.io/An-Annotated-Proof-of-Generative-Adversarial-Networks-with-Implementation-Notes/
3. https://arxiv.org/pdf/1701.00160.pdf
4. https://www.uio.no/studier/emner/matnat/ifi/IN5400/v21/lecture-slides/in5400_2021_slides_gans_lecture14.pdf
5. https://www.cs.toronto.edu/~duvenaud/courses/csc2541/slides/gan-foundations.pdf
6. http://cs231n.stanford.edu/slides/2017/cs231n_2017_lecture13.pdf
7. https://arxiv.org/pdf/1406.2661.pdf
8. https://deepgenerativemodels.github.io/notes/gan/
9. https://proceedings.neurips.cc/paper/2014/file/5ca3e9b122f61f8f06494c97b1afccf3-Paper.pdf