Written by MMA
on August 23, 2019
8 mins to read.

Generative and Discriminative models

In this article we discuss basic differences between Generative and Discriminative models. Actually, so far, we have already seen couple of those models, which Logistic Regression is one of the well-known discriminative classifiers whereas Naive Bayes algorithm is one for generative ones. Here’s the most important part from the lecture notes of CS299 (by Andrew Ng) related to the topic, which really helps to understand the difference between discriminative and generative learning algorithms.

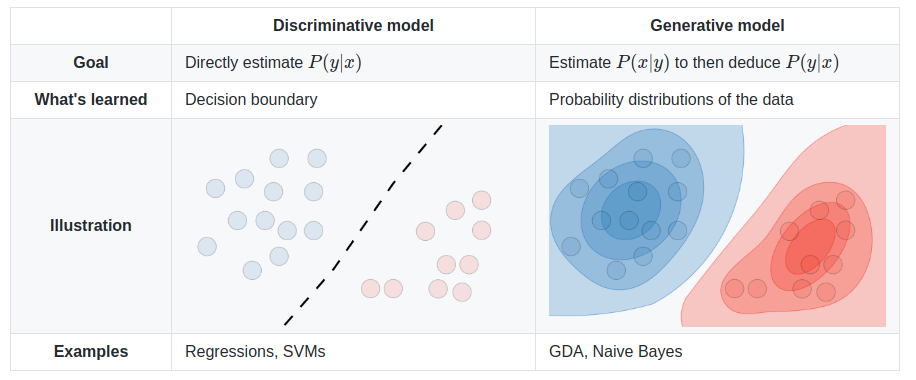
It is important to understand the difference between Generative and Discriminative models because with growing number of classifiers in the literature, it is becoming impossible to rely on trial-error method where we try to find the most optimal algorithm for a particular dataset. Thus, based on what one wishes to achieve from the analysis, classifiers are broadly divided into these two groups: (1) Discriminative models, and (2) Generative models. The fundamental difference between these models is: (1) Disriminative models learn the explicit (hard or soft) boundaries between classes (and not necessarily in a probabilistic manner), (2) Generative models learn the distribution of individual classes, therefore, providing a model of how the data is actually generated, in terms of a probabilistic model. (e.g., logistic regression, support vector machines or the perceptron algorithm simply give you a separating decision boundary, but no model of generating synthetic data points).

Think of an analogy. The task is to determine the language that someone is speaking. Generative approach is used to learn each language and determine as to which language the speech belongs to. Discriminative approach is used to determine the linguistic differences without learning any language, which is a much easier task!

So far, we’ve mainly been talking about learning algorithms that model $P(y \mid X, \theta)$, the conditional distribution of $y$ given $x$. For instance, logistic regression models $P(y \mid X, \theta)$ as $h_{\theta}(x) = \sigma(\theta^{T} X)$ where $\sigma$ is the sigmoid function. In essence, you’re just applying a logistic function to a dot product.

Consider a classification problem in which we want to learn to distinguish between elephants ($y = 1$) and dogs ($y = 0$), based on some features of an animal. Given a training set, an algorithm like logistic regression or the perceptron algorithm (basically) tries to find a straight line -that is, a decision boundary- that separates the elephants and dogs. Then, to classify a new animal as either an elephant or a dog, it checks on which side of the decision boundary it falls, and makes its prediction accordingly.

Here’s a different approach. First, looking at elephants, we can build a model of what elephants look like. Then, looking at dogs, we can build a separate model of what dogs look like. Finally, to classify a new animal, we can match the new animal against the elephant model, and match it against the dog model, to see whether the new animal looks more like the elephants or more like the dogs we had seen in the training set.

Algorithms that try to learn $P(y \mid X)$ (posterior probabilities) directly, or algorithms that try to learn mapping functions directly from the space of inputs $X$ to output (the labels ${0, 1}$), are called discriminative learning algorithms since the conditional distribution discriminates directly between the different values of $y$, whereas algorithms which tries to model $P(X \mid y)$ (class conditionals probability distribution functions, and of course, class prior probabilities $P(y)$) are called generative learning algorithms.

Assume that $y$ indicates whether an example is a dog (0) or an elephant (1), then $P(X \mid y = 0)$ models the distribution of dogs’ features, and $P(X \mid y = 1)$ models the distribution of elephants’ features.

After computing $P(y)$ and $P(X \mid y)$, a generative algorithm can then use Bayes’ rule to derive the posterior distribution on $y$ given $X$:

\[P(y \mid X) = \frac{P(X, y)}{P(X)} = \frac{P(X \mid y) P(y)}{P(X)}\]

Here, the denominator is given by $P(X) = P(X \mid y = 0)P(y=0) + P(X \mid y = 1)P(y=1)$ (you should be able to verify that this is true from the standard properties of probabilities), and thus can also be expressed in terms of the quantities $P(X \mid y)$ and $P(y)$ that we’ve learned. Actually, if were calculating $P(y \mid X)$ in order to make a prediction, then we don’t actually need to calculate the denominator, since,

\[\underset{y}{\operatorname{argmax}} P(y \mid X) = \underset{y}{\operatorname{argmax}} \frac{P(X \mid y) P(y)}{P(X)} = \underset{y}{\operatorname{argmax}} P(X \mid y) P(y)\]

After we calculate the posterior probabilities, we pick the most likely label $y$ for this new test data.

Differences

As one can see easily that a discriminative classifier tries to model by just depending on the observed data. It makes fewer assumptions on the distributions but depends heavily on the quality of the data (Is it representative? Are there a lot of data?). Generative algorithms make some structural assumptions on the model. For example, Naive Bayes classifier assumes conditional independence of the features. Generative models can actually learn the underlying structure of the data if you specify your model correctly and the model actually holds, but discriminative models can outperform in case your generative assumptions are rarely satisfied (since discriminative algorithms are less tied to a particular structure, and the real world is messy and assumptions are rarely perfectly satisfied anyways).

Intuitively, we can say generative algorithms is typically overfitting less because it allows the user to put in more side information in the form of class conditionals.

The discriminative model is more sensitive to outliers as we model the boundaries. Each outlier will shift the class boundaries.

By estimating $P(y, X)$ and being able to sample $X$, $y$ pairs - a generative model can be used to impute missing data, compress your dataset or generate unseen data.

Additionally, when training data is biased over one class, in generative learning algorithms, wrong model assumption will be made since generative algorithms make some structural assumptions on the model. The joint probability will be biased as class probabilities will be biased. Thus, the conditional probability will be biased, too. Similarly, in discriminative models, we will receive biased conditional probability.

There are several compelling reasons for using discriminative rather than generative classifiers, one of which, succinctly articulated by Vapnik, is that “one should solve the classification problem directly, and never solve a more general problem as an intermediate step (such as modelling $P(y \mid X)$)”, meaning that discriminative methods attack the problem directly. Indeed, leaving aside computational issues and matters such as handling missing data, the prevailing consensus seems to be that the discriminative classifiers are almost always preferred to generative ones. However, you gain little understanding about the data from discriminative models.

Note that generative algorithms may have discriminative properties, since you can get $P(y \mid X)$ once you have $P(X \mid y)$ and $P(y)$ (by Bayes’ Theorem), though discriminative algorithms do not really have generative properties.

Since generative models model each class separately they can be trained on a per-class basis. This can be a huge benefit in some case, especially when there is a thousands of categories. The model for each category can be trained independently, you don’t even need to define all the categories in advance— just train on whatever you have. As new categories and their training sets get added, train additional models — specific to the new ones. Discriminative learning does not work so well in this setting. Since it’s trying to learn what distinguishes all the classes, it needs to be trained on a single training set with all observations included.

Although, discriminative methods give good predictive performance and have been widely used in many applications (e.g., discriminative models usually tend to do better when labelled training data is plentiful; generative models may be better if you have some extra unlabeled data, because, although collection of data is often easy, the process of labelling it can be expensive. Consequently there is increasing interest in generative methods since these can exploit unlabelled data in addition to labelled data), there also exists hybird models too that try to bring in the best of both worlds.

Specific Algorithms Of Each Type

Commonly used discriminative learning algorithms include Support-vector machines, logistic regression, and decision trees; ensemble methods, i.e., random forest and gradient boosting; multi-layer perceptrons and, the top-most layers of deep neural networks. Interestingly, lower layers of deep learning algorithms are often generative; upper layers often discriminative.

The most commonly used generative algorithm is the naive Bayes classifier. Besides, Bayesian networks, Markov random fields and Hidden Markov Models (HMM) are examples of this type.

REFERENCES

← → Top