Implementing 'SAME' and 'VALID' padding of Tensorflow in Python

While using convolutional neural network, we don’t have to manually calculate the dimension (the spatial size) of the output(s), but it’s a good idea to do so to keep a mental account of how our inputs are being transformed at each step. We can compute the spatial size on each dimension (width/height/depth(channel)).

1. The input volume size (input width $W_{1}$ and input height $H_{1}$, generally they are equal and input depth $D_{1}$)
2. Number of filters ($K)$
3. The receptive field size of filter. You can have different filters horizontally and vertically ($F_{w}$ for width and $F_{h}$ for height).
4. The stride with which they are applied. You can have different strides horizontally and vertically ($S_{w}$ for width and $S_{h}$ for height)
5. The amount of zero padding used ($P$) on the border.

produces an output of shape $W_{2} \times H_{2} \times D_{2}$ where:

$W_{2} = \dfrac{W_{1} - F_{w} + 2P}{S_{w}} + 1$

$H_{2} = \dfrac{H_{1} - F_{h} + 2P}{S_{h}} + 1$ (i.e., width and height are computed equally by symmetry)

$D_{2}= K$

Note that $2P$ comes from the fact that there should be a padding on each side, left/right and top/bottom.

However, the height or width of the output image, calculated from these equations, might be a non-integer value. In that case, you might want to handle the situation in any way to satisfy the desired output dimention. Here, we explain how Tensorflow approaches this issue. The spatial semantics of the convolution ops depend on the padding scheme chosen: ‘SAME’ or ‘VALID’. Note that the padding values are always zero.

Let’s assume that the 4D input has shape [batch_size, input_height, input_width, input_depth], and the 4D filter has shape [filter_height, filter_width, filter_depth, number_of_filters]. Here, the number of channels (depth) in input image must be the same with the depth of the filter, meaning input_depth = filter_depth.

First let’s consider 'SAME' padding scheme. The output height and width are computed as:

Here, $\left \lceil \cdot \right \rceil$ is the ceiling function.

Here is how Tensorflow calculates the required total padding, applied along the height and width:

if $H_{1} \% S_{h} == 0$:

else:

Similarly, for padding along the width,

if $W_{1} \% S_{w} == 0$:

else:

Here, $\%$ represents modulo operation. In computing, the modulo operation finds the remainder after division of one number by another (sometimes called modulus).

Finally, the padding on the top/bottom and left/right are:

Note that the division by 2 means that there might be cases when the padding on both sides (top vs bottom, right vs left) are off by one. In this case, the bottom and right sides always get the one additional padded pixel.

For example, when padding along height is 5, we pad 2 pixels at the top and 3 pixels at the bottom. Note that this is different from existing libraries such as cuDNN and Caffe, which explicitly specify the number of padded pixels and always pad the same number of pixels on both sides.

Similarly, in the 'VALID' padding scheme which we do not add any zero padding to the input, the size of the output would be:

Again, $\left \lceil \cdot \right \rceil$ is the ceiling function.

What’s an image?

Generally, we can consider an image as a matrix whose elements are numbers between 0 and 255. The size of this matrix is $\text{image height} \times \text{image width} \times \text{image depth}$. A grayscale image has 1 channel (such as infamous MNIST dataset) where a color image has 3 channels (for an RGB). Based on the input, a convolution layer can have either multiple input channels (each is a 2D matrix) or one input channel (still a 2D matrix) and resulting layer can have either multiple output channels (multiple kernel, again, each is a 2D matrix) or one output channel (one kernel, still a 2D matrix).

Each convolution acts like a feature-extractor over the image. The number of output channels defines the number of kernels, which convolve over your input volume. So even if your input image is a grayscale image (1 channel), a lot of different kernels can learn different things. In any case, computations are almost similar with a slight tweak.

When the input has 3 channels, we will have 3 filters (one for each channel) instead of one channel. Then, we calculate the convolution of each filter with its corresponding input channel (First filter with first channel, second filter with second channel and so on). The stride of all channels are the same, so they output matrices with the same size. Now, we can sum up all matrices and output a single matrix which is the only channel at the output of the convolution layer.

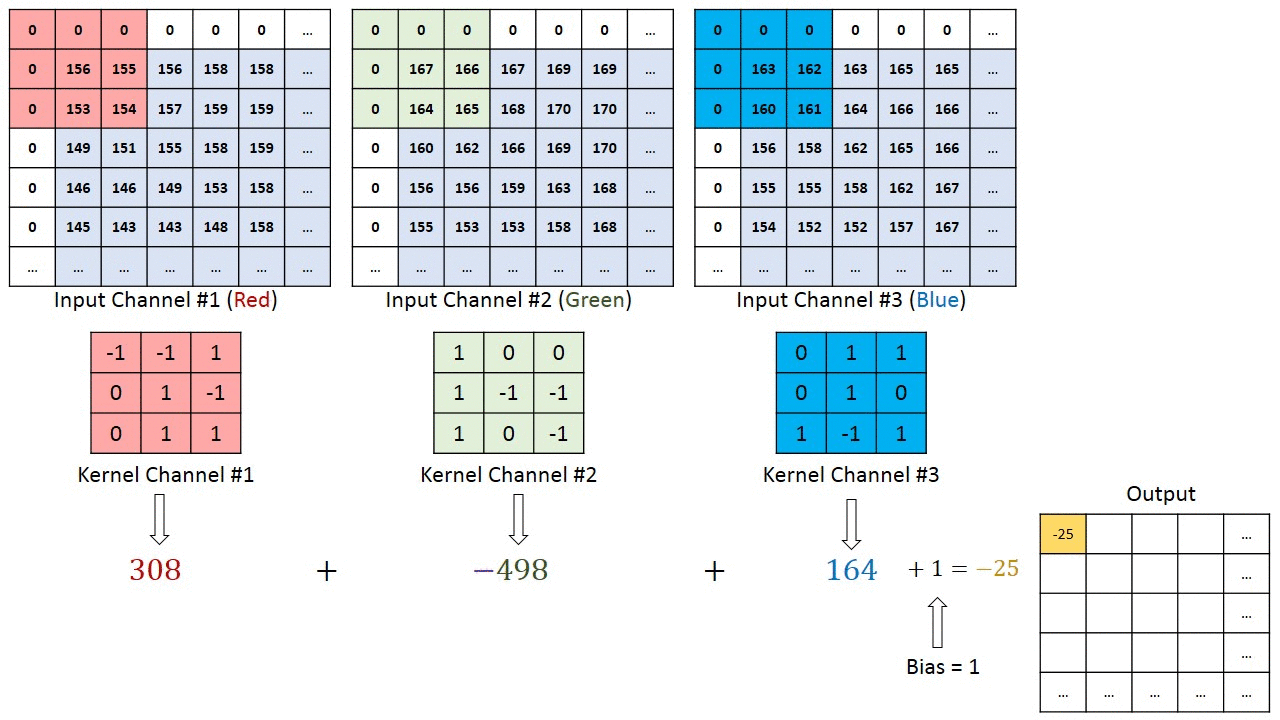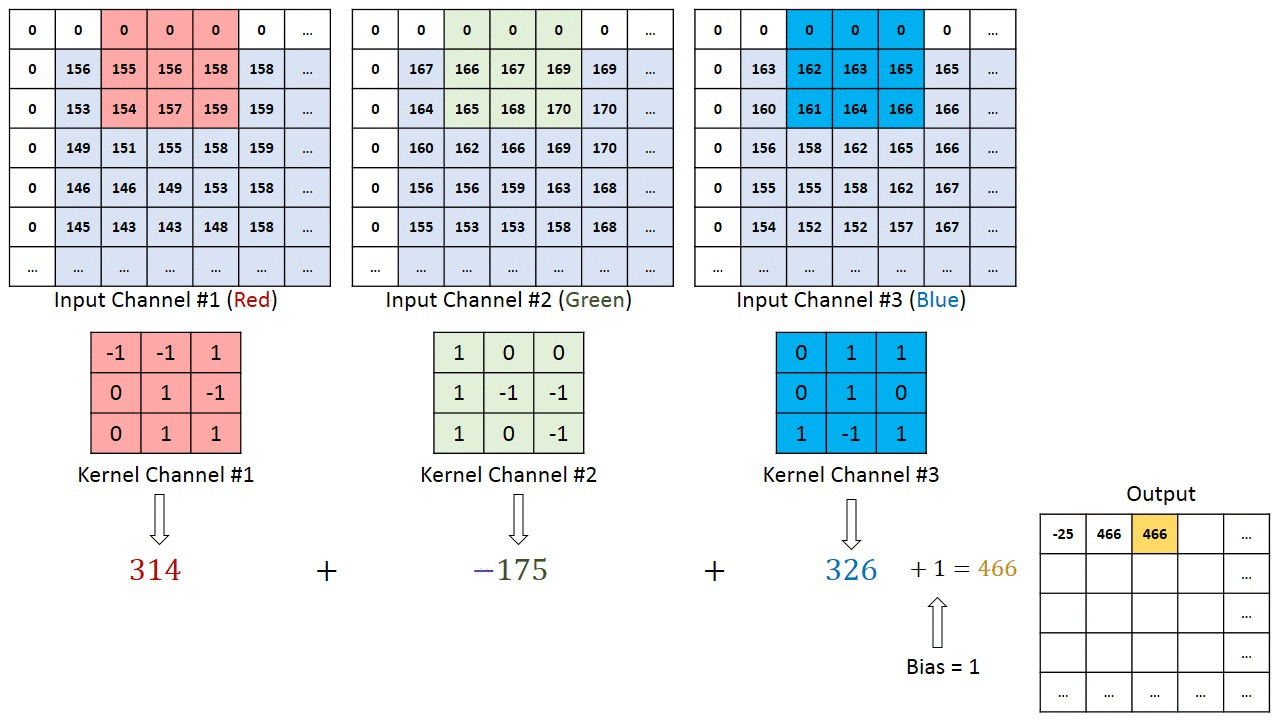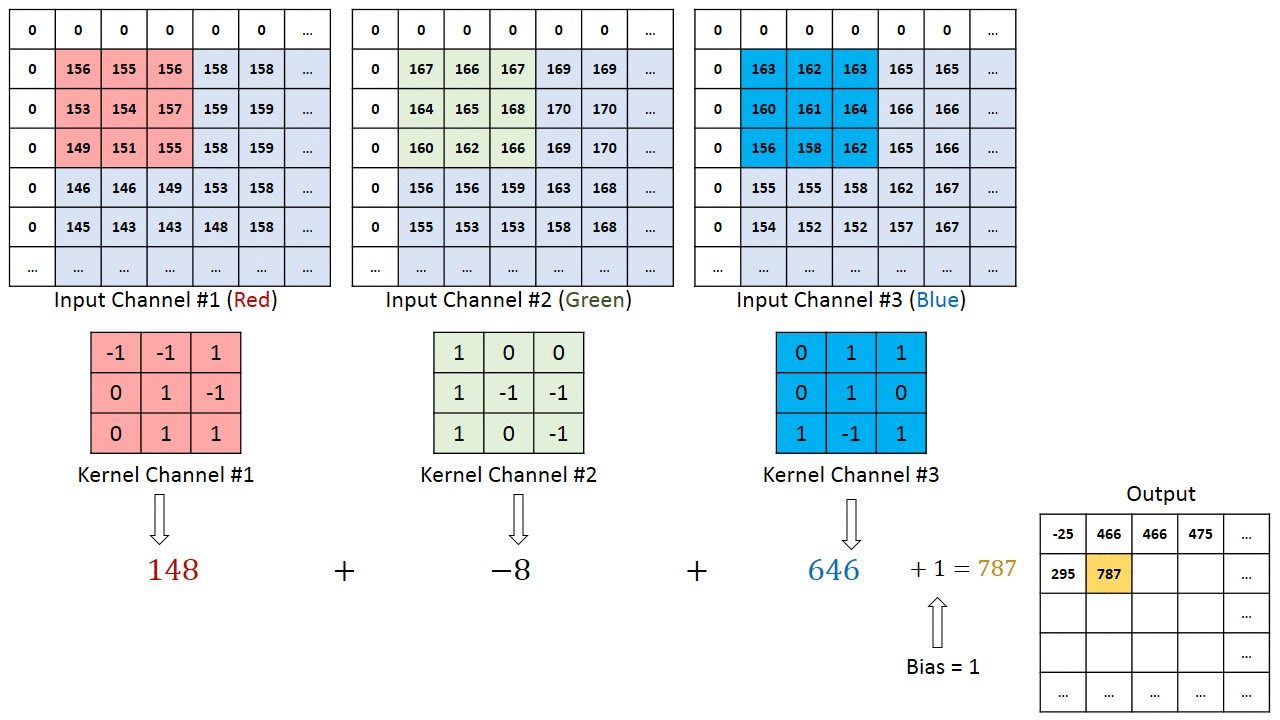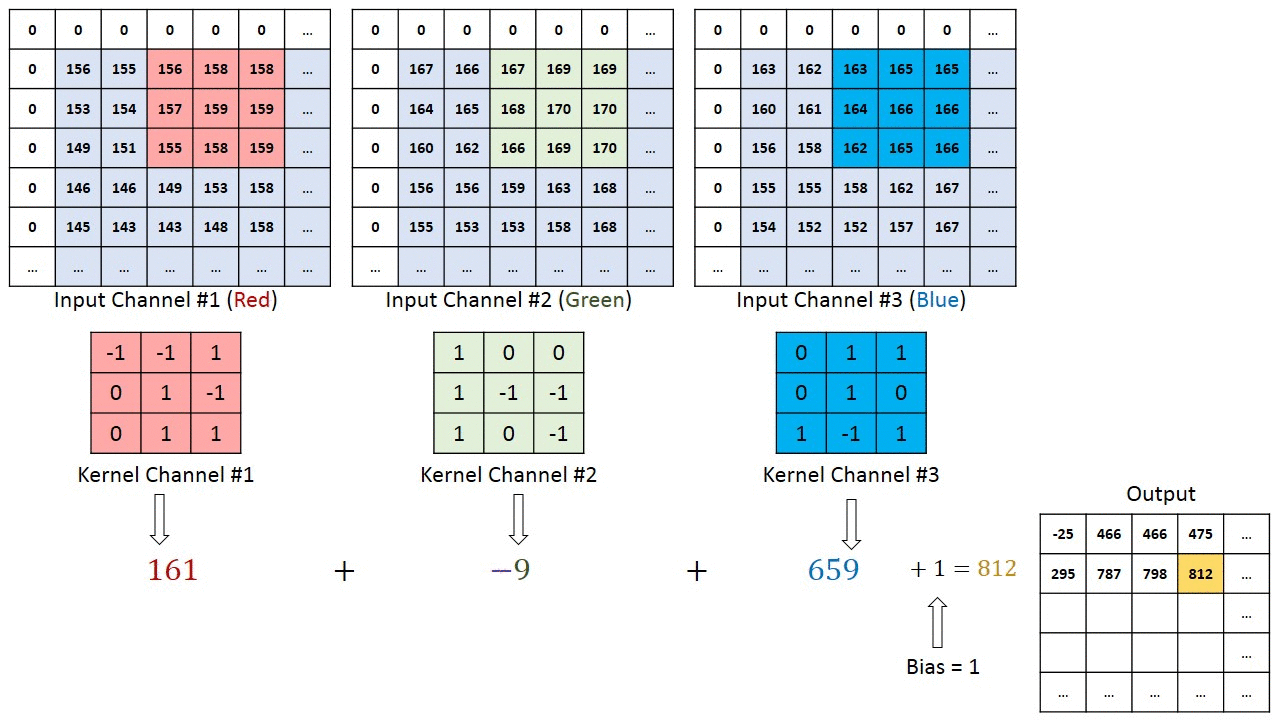
Implementing Convolution Operator in Python

Implementing convolution operator in Python is pretty straight forward. Here, we will use a image from sklearn datasets. The shape of the image is (427, 640, 3), which means that its height is 427, its width is 640 and it consists of three input channels, RGB image.

from sklearn.datasets import load_sample_image
china = load_sample_image("china.jpg")

plt.imshow(china)
plt.savefig('china.jpg')

We are going to use $7 \times 7 \times 3$ filters (kernels/weights) (One with a vertical line in the middle, and the other with horizontal white line in the middle). We will apply them to the image using a convolutional layer built using Tensorflow’s tf.nn.conv2d() function and our python implementations with a stride of 2.

filters = np.zeros(shape=(7, 7, 3, 2), dtype=np.float32)
filters[:, 3, :, 0] = 1#vertical line
filters[3, :, :, 1] = 1#horizontal line

plt.imshow(filters[:,:,0,0], cmap="gray", interpolation="nearest")
plt.show()
plt.imshow(filters[:,:,0,1], cmap="gray", interpolation="nearest")
plt.show()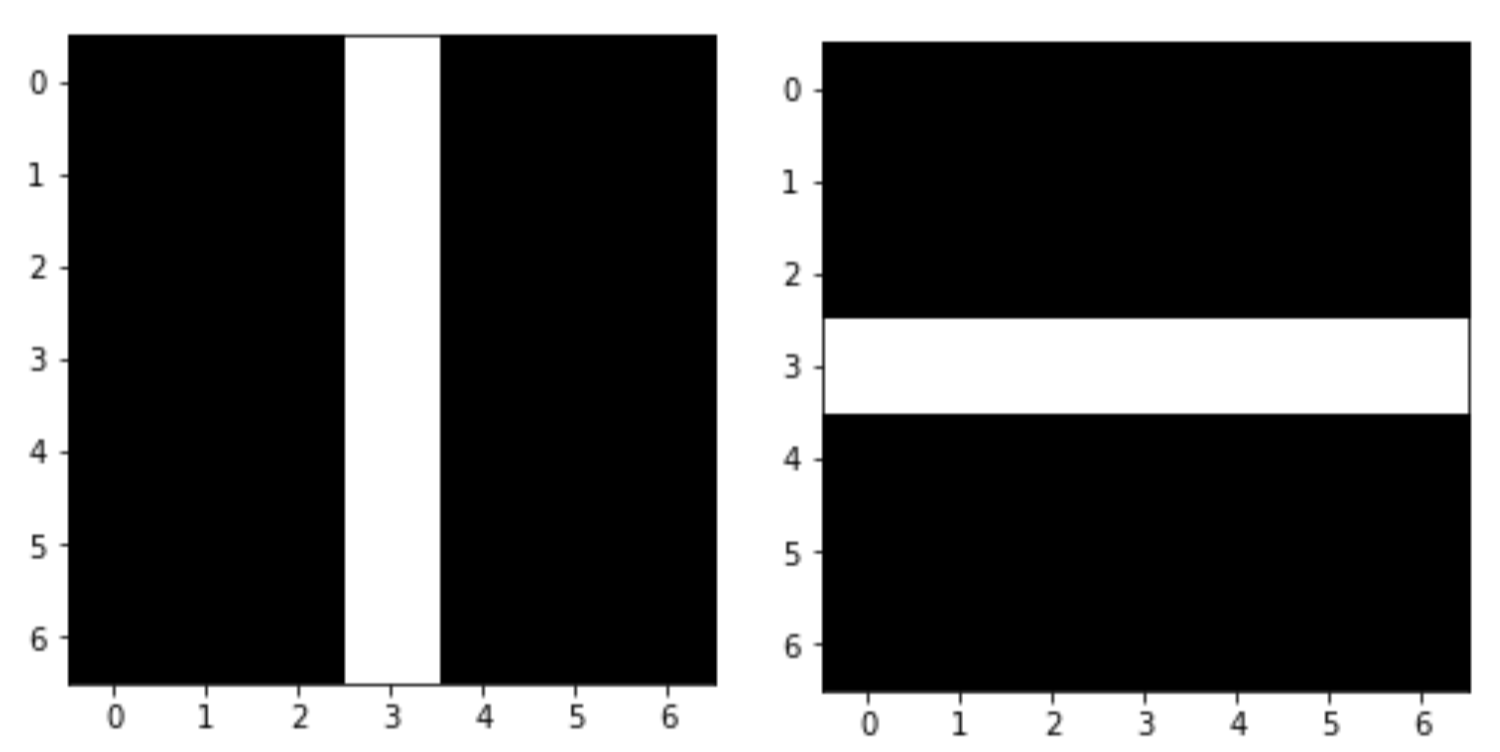

Single Feature Map (Single Output Channel)

For this implementation, the shape of the input must be [input_height, input_width, input_depth] and the shape of the filter must be [filter_height, filter_width, filter_depth] since we have only one filter.

Multiple Feature Maps (Multiple Output Channels)

For this implementation, the shape of the input must be [input_height, input_width, input_depth] and the shape of the filter must be [filter_height, filter_width, filter_depth, number_of_filters] since we have multiple filters.

tf.nn.conv2d()

Tensorflow’s tf.nn.conv2d() accepts:

1. input, which is a input mini-batch, a 4D tensor shape of [batch_size, input_height, input_width, input_depth]. In our case, batch_size will be 1 because we are only using one image.

2. filters is the set of filters to apply. They are represented as a 4D tensor of shape [filter_height, filter_width, filter_depth, number_of_filters]. If we use one filter, number_of_filters argument will equal to 1. If we have multiple filters, say, K, we will have K feature maps (K output channels - the depth of the output layer will be K).

3. strides is a four-element 1D array, where the two central elements are the vertical and horizontal strides ($S_{h}$ and $S_{w}$). The first and the last elements must currently be equal to 1. They may one day be used to specify a batch stride (to skip some instances) and a channel stride (to skip some of the previous layer’s feature maps or channels).

4. padding must be either 'VALID' or 'SAME' which we explained them earlier.

Comparisons

For using both one filter and multiple filters, if we compare our Python implemetations with Tensorflow’s, we will see that the output arrays are the same.

#One filter on RGB image
from sklearn.datasets import load_sample_image
china = load_sample_image("china.jpg")
height, width, depth = china.shape

##################################################################################

filter = np.zeros(shape=(7, 7, depth, 1), dtype=np.float32)
#We use one filter.
filter[:, 3, :, 0] = 1 #vertical line

output1 = convolution2d(china, filter[:,:,:,0], bias=0, strides = (2,2), padding='SAME')

##################################################################################

import tensorflow as tf

image = china.reshape((-1, height, width, depth))

X= tf.placeholder(tf.float32, shape=(None, height, width, depth))
convolution = tf.nn.conv2d(input = X, filter = filter, strides = [1,2,2,1], padding="SAME")

with tf.Session() as sess:
    output2 = sess.run(convolution,feed_dict = {X: image})
    
##################################################################################

np.array_equal(output2[0, :, :, 0], output1)
#True

#Multiple filter on RGB image
from sklearn.datasets import load_sample_image
china = load_sample_image("china.jpg")
height, width, depth = china.shape

##################################################################################

filters = np.zeros(shape=(7, 7, depth, 2), dtype=np.float32)
filters[:, 3, :, 0] = 1#vertical line
filters[3, :, :, 1] = 1#horizontal line

output1 = multi_convolution2d(china, filters, strides = (2,2), padding='SAME')

##################################################################################

import tensorflow as tf

image = china.reshape((-1, height, width, depth))

X= tf.placeholder(tf.float32, shape=(None, height, width, depth))
convolution = tf.nn.conv2d(input = X, filter = filters, strides = [1,2,2,1], padding="SAME")

with tf.Session() as sess:
    output2 = sess.run(convolution,feed_dict = {X: image})
    
##################################################################################

np.array_equal(output2[0, :, :, :], output1)
#True

A Note on TensorFlow’s tf.nn.conv2d

TensorFlow’s tf.nn.conv2d function has an argument data_format which is an optional string from: “NHWC”, “NCHW”. NHWC is by default. NHWC simply means the order of dimensions in a 4D tensor, which is:

N: batch

H: height (spatial dimension)

W: width (spatial dimension)

C: number of channels of the image (ex: 3 for RGB, 1 for grayscale…) (depth)

NHWC is the default layout for TensorFlow; another commonly used layout is NCHW, because it’s the format preferred by NVIDIA’s DNN libraries.

References

1. https://www.tensorflow.org/api_guides/python/nn#Convolution
2. https://www.tensorflow.org/api_guides/python/nn#Notes_on_SAME_Convolution_Padding