8 dakikada okunabilir.
Gower Uzaklığı
Uzaklık ölçütleri (distance measures) makine öğrenmesinde önemli bir rol oynamaktadır. K-en yakın komşular (K-nearest neighbors) algoritmasının da parçası olduğu denetimli öğrenme (supervised learning) teknikleri; K-ortalamalar (K-means) algoritmasının da parçası olduğu denetimsiz öğrenme (unsupervised learning) teknikleri ve Destek Vektör Makineleri algoritmasının da parçası olduğu çekirdek-tabanlı (kernel-based) yöntemler gibi birçok popüler ve etkili makine öğrenmesi algoritması için temel sağlarlar. Bu nedenle, veri tiplerine göre farklı uzaklık ölçüleri seçilmeli ve kullanılmalıdır.
Bir uzaklık ölçütü, bir problem alanında iki nesne arasındaki göreli farkı özetleyen nesnel bir skordur. En yaygın olarak, iki nesne bir özneyi (bir kişi, araba veya ev gibi) veya bir olayı (satın alma, talep veya teşhis gibi) tanımlayan veri satırlarıdır.
İki örnek (veya veri satırı) arasındaki uzaklığı hesaplarken, bu örneklerin farklı sütunları (değişkenleri veya öznitelikleri) için farklı veri tiplerinin kullanılması mümkündür. Bir örneğin değişkenleri reel değerlere, boole değerlerine, kategorik değerlere ve ordinal (sıra) değerlere sahip olabilir. Her bir farklı değişken için farklı mesafe ölçütleri gerekebilir.
Gower Uzaklığı (Gower’s Distance) karışık-tip (mixed-type) değişkenlerden (özniteliklerden) oluşan bir veri kümesindeki iki satır (veya gözlem) arasındaki benzerliği bulmak için kullanılan bir ölçüttür (measure). Gower’ın uzaklık ölçütü, her değişken için farklı olarak $x_i$ ve $x_j$ örnekleri arasındaki uzaklığın bileşenlerini hesaplayarak bunu yapabilir. Öklid Uzaklığı (Euclidean Distance), Manhattan Uzaklığı (Manhattan distance) veya Kosinüs Uzaklığı gibi, Gower Uzaklığı da bir mesafe ölçütüdür.
Diyelim ki $x_i = (x_{i1}, \dots, x_{ip})$ ve $x_j = (x_{j1}, \dots, x_{jp})$ gibi iki gözlem var ve bu gözlemlerin birbirlerine ne kadar benzer (similar) (veya benzemez (dissimilar)) olduğunu ölçmek istiyoruz.
Bu iki vektördeki girdilerin her biri nicel ise (yani gerçek sayı değerlerini alıyorsa), o zaman Öklid Uzaklığı (Euclidean Distance) veya Manhattan Uzaklığı (Manhattan distance) gibi bir kaç uzaklık ölçütünü bir benzerlik (similarity) veya benzersizlik (dissimilarity) ölçüsü olarak kullanabiliriz. Peki ya elimizdeki veri kümesindeki $p$ değişkenin (özniteliğin) tümü sayısal değilse? Ya bazıları kategorik (categorical) veya ikili (binary) ise?
Gower (1971) makalesinde tanıtılan Gower Uzaklığı, bu durumda kullanılabilecek genel bir benzerlik ölçüsüdür. Her öznitelik $k = 1, \dots, p$ için, bir $s_{ijk} \in [0,1]$ skoru hesaplanır. $x_i$ ve $x_j$, $k$ özniteliği boyunca birbirine yakınsa (birbirine benzerse), $s_{ijk}$ skoru 0’a yakındır. Tersine, $k$ özniteliği boyunca bu iki gözlem birbirinden uzaklarsa (birbirlerine benzer değilse), $s_{ijk}$ skoru 1’a yakındır.
$s_{ijk}$ skorunun nasıl hesaplandığı, $k$ özniteliğinin tipine bağlıdır. Ayrıca, bir $\delta_{ijk}$ değeri de hesaplanır: eğer $x_i$ ve $x_j$, $k$ özniteliği boyunca karşılaştırılabilirse, o zaman $\delta_{ijk} = 1$. Eğer $x_i$ ve $x_j$, $k$ özniteliği boyunca karşılaştırılamazsa (örneğin, kayıp gözlemler nedeniyle), $\delta_{ijk}$ sıfıra ayarlanır. Gower Uzaklığı ise sadece (bilinen/hesaplanan) skorların ortalamasıdır:
\[S_{i j}=\frac{\sum\limits_{k=1}^{p} s_{i j k} \, \delta_{i j k}}{\sum\limits_{k=1}^{p} \delta_{i j k}}\]Şimdi, her bir öznitelik tipi için skorların nasıl hesaplanacağı hakkında konuşalım. Gower, 3 farklı öznitelik tipi tanımlar:
- Nicel değişkenler (sayısal/nümerik değişkenler): $s_{ijk} = \dfrac{\mid x_{ik} - x_{jk} \mid}{R_{k}}$, burada $R_k$, popülasyondaki veya örneklemedeki $k$-ıncı özniteliğin aralığıdır (range).
- Nitel değişkenler (kategorik değişkenler): Eğer ${ x_{ik} = x_{jk} }$ ise, $s_{ijk} = 0$. Eğer ${ x_{ik} \neq x_{jk} }$ ise $s_{ijk} = 1$.
Gower Uzaklığını hesaplamak için Python’un gower modülü kullanılabilir (https://pypi.org/project/gower/). Bu modül her bir satır ile diğer satırlar arasındaki Gower Uzaklığını hesaplayarak size bir matris döndürecektir. Ancak, bu değerlerin nasıl hesaplandığını görmek için el ile çözüm de aşağıda gösterilmiştir.
8 gözlemden ve 5 öznitelikten oluşan bir veri kümesine sahip olduğumuzu varsayalım:
import pandas as pd
import gower
data = {'age': [14, 19,10, 14, 21, 19, 30, 35],
'preTestScore': [4, 24, 31, 3, 3, 4, 31, 9],
'postTestScore': [25, 94, 57, 30, 70, 25, 69, 95],
'availableCredit': [2200, 1000, 2200, 2100, 2000, 1000, 6000, 2200],
'gender': ['M', 'M', 'M', 'M', 'F', 'F', 'F', 'F']}
df = pd.DataFrame(data)
df
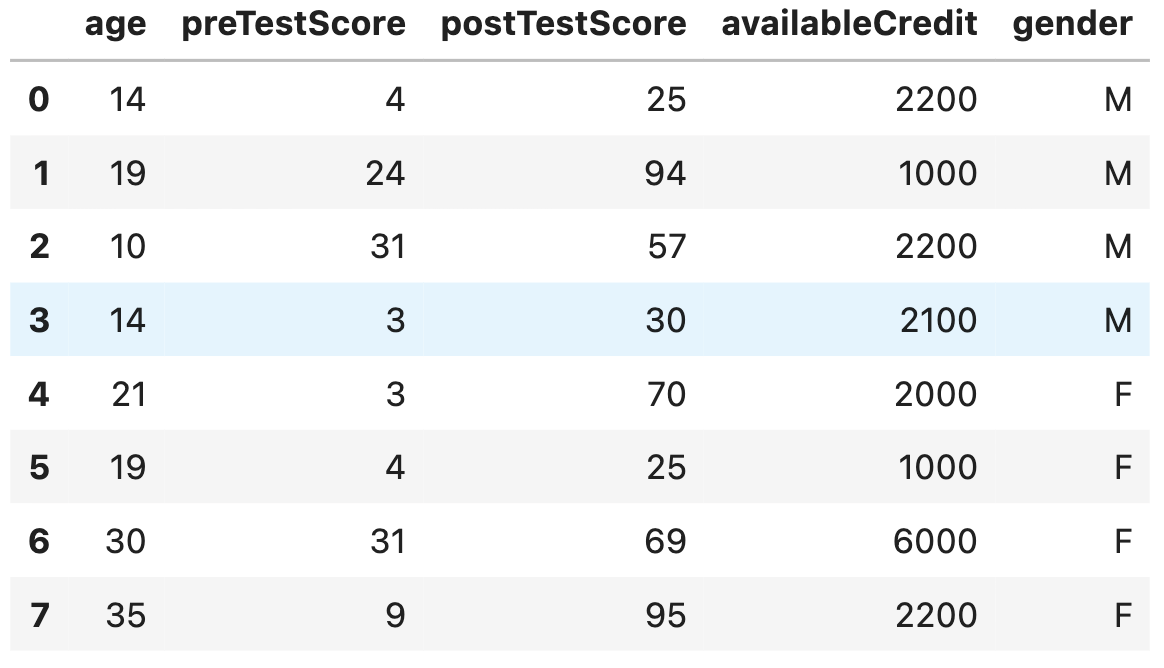
gower modülünde bulunan gower_matrix fonksiyonunu kullanarak her bir gözlem ile diğer gözlemler arasındaki Gower Uzaklıkları bir matris olarak hesaplanabilir:
pd.DataFrame(gower.gower_matrix(df), index = ['Satır ' + str(i+1) for i in range(df.shape[0])], columns = ['Satır ' + str(i+1) for i in range(df.shape[0])])

Veri kümesinde 8 adet satır (diğer bir deyişle 8 farklı gözlem) olduğundan, gower_matrix fonksiyonunun çıktısı $8 \times 8$ boyutlu bir matris olacaktır. Bu matrisin simetrik olduğu kolaylıkla görülebilir. Bu matrise Uzaklık Matrisi (Distance Matrix) denir.
Elde edilen bu matrisinin elemanlarının nasıl kolaylıkla el ile hesaplanabileceğine bir göz atalım. Tabii ki, bu matrisin tüm elemanlarını el ile hesaplamamıza gerek yok. Sadece yukarıda verilen formülasyonun nasıl çalıştığını görebilmemiz için.
El ile hesaplamaya geçmeden önce Gower Uzaklığı’nın ihtiyaç duyduğu gibi, nümerik değişkenlerin aralıklarını (yani, $R_k$’ları) hesaplayalım. Veri kümesindeki nümerik değişkenler df.select_dtypes('number') kod satırı ile kolaylıkla elde edilebilir. Bir değişkenin aralığı, o değişkenin maksimum değeri ile minimum değeri arasındaki farktır:
df_numeric = df.select_dtypes('number')
pd.DataFrame(df_numeric.max() - df_numeric.min(), columns = ['Aralık'])

Burada, i = 1, 2, .., 8 ve j= 1, 2, ..., 8 ve 5 tane değişkenimiz olduğu için k = 1, 2, 3, 4, 5‘tir.
İlk iki satırın (yani ilk iki gözlemin) birbirine ne kadar benzer olup olmadığını Gower Uzaklığı ile elde edelim. Yani, 0.428000 değerini el ile bulmaya çalışalım. Bu durumda, i = 1 ve j= 2‘dir. Bu nedenle, $s_{1, 2, k}$ değerlerini tüm öznitelikler için ($k = 1, 2, 3, 4, 5$) hesaplamamız gerekmektedir.
age değişkeni için, yani, $k = 1$
age değişkeni nümerik bir değişkendir. Bu nedenle, $s_{121} = \dfrac{\mid x_{11} - x_{21} \mid}{R_{1}}$. Burada, $x_{11} = 14$ ve $x_{21} = 19$’dur. $R_{1}$ ise age değişkeninin aralığıdır (range). Yukarıda hesapladığımız gibi, age değişkenin aralığı 25’tir. Bulduğumuz değerler, yerlerine koyarsak, $s_{121} = \dfrac{\mid x_{11} - x_{21} \mid}{R_{1}} = \dfrac{\mid 14 - 19 \mid}{25} = 0.2$ elde ederiz.
preTestScore değişkeni için, yani, $k = 2$
preTestScore değişkeni nümerik bir değişkendir. Bu nedenle, $s_{122} = \dfrac{\mid x_{12} - x_{22} \mid}{R_{2}}$. Burada, $x_{12} = 4$ ve $x_{22} = 24$’dur. $R_{2}$ ise preTestScore değişkeninin aralığıdır (range). Yukarıda hesapladığımız gibi, preTestScore değişkenin aralığı 28’tir. Bulduğumuz değerler, yerlerine koyarsak, $s_{122} = \dfrac{\mid x_{12} - x_{22} \mid}{R_{2}}= \dfrac{\mid 4 - 24 \mid}{28} = 0.7142857142857143$ elde ederiz.
postTestScore değişkeni için, yani, $k = 3$
postTestScore değişkeni nümerik bir değişkendir. Bu nedenle, $s_{123} = \dfrac{\mid x_{13} - x_{23} \mid }{R_{3}}$. Burada, $x_{13} = 25$ ve $x_{23} = 94$’dur. $R_{3}$ ise postTestScore değişkeninin aralığıdır (range). Yukarıda hesapladığımız gibi, postTestScore değişkenin aralığı 70’tir. Bulduğumuz değerler, yerlerine koyarsak, $s_{123} = \dfrac{\mid x_{13} - x_{23} \mid }{R_{3}} = \dfrac{ \mid 25 - 94 \mid}{70} = 0.9857142857142858$ elde ederiz.
availableCredit değişkeni için, yani, $k = 4$
availableCredit değişkeni nümerik bir değişkendir. Bu nedenle, $s_{124} = \dfrac{\mid x_{14} - x_{24} \mid }{R_{4}}$. Burada, $x_{14} = 2200$ ve $x_{24} = 1000$’dur. $R_{4}$ ise availableCredit değişkeninin aralığıdır (range). Yukarıda hesapladığımız gibi, availableCredit değişkenin aralığı 5000’tir. Bulduğumuz değerler, yerlerine koyarsak, $s_{124} = \dfrac{\mid x_{14} - x_{24} \mid }{R_{4}}= \dfrac{\mid 2200 - 1000 \mid}{5000} = 0.24$ elde ederiz.
gender değişkeni için, yani, $k = 5$
gender değişkeni kategorik bir değişkendir. $x_{15} = ‘M’$ ve $x_{25} = ‘M’$’dir. $x_{15} = x_{25}$ olduğundan, $s_{125} = 0$’dir.
Gower Uzaklığı, yukarıda hesapladığımız skorların ortalamasıdır.
O halde,
\[S_{12} = \frac{0.2 + 0.7142857142857143+ 0.9857142857142858 + 0.24 + 0}{5} = 0.4280\]Birinci gözlem ile ikinci gözlem arasındaki Gower Uzaklık ölçümü 0.4280 elde edilmiştir. Dikkat edilirse, el ile bulduğumuz değer, gower modülünde bulunan gower_matrix fonksiyonunun çıktısı ile aynıdır. Aynı hesaplamalar diğer matris hücreleri için benzer şekilde gerçekleştirilebilir.
REFERENCES
- https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.412.4155&rep=rep1&type=pdf
- https://www.math.vu.nl/~sbhulai/papers/thesis-vandenhoven.pdf
- https://www.thinkdatascience.com/post/2019-12-16-introducing-python-package-gower/
- https://rstudio-pubs-static.s3.amazonaws.com/423873_adfdb38bce8d47579f6dc916dd67ae75.html#fnref2
- https://towardsdatascience.com/clustering-on-mixed-type-data-8bbd0a2569c3
- https://statisticaloddsandends.wordpress.com/2021/02/23/what-is-gowers-distance/