Döngüsel Yapıya Sahip Değişkenleri Nasıl Kodlarız?

Doğası gereği bazı veriler döngüsel (cyclical) bir yapıya sahiptir. Zaman (time) bunun çok güzel bir örneğidir: dakika, saat, saniye, haftanın günü, ayın haftası, ay, mevsim vb. tüm değişkenler bir döngüyü (cycle) takip etmektedir. Gelgit gibi ekolojik değişkenler, yörüngedeki konum gibi astrolojik değişkenler, rotasyon veya boylam gibi uzamsal değişkenler, renk çarkları gibi görsel değişkenler doğal olarak döngüseldir. Peki, makine öğrenimi modelimizin bir özelliğin döngüsel olduğunu bilmesini nasıl sağlayabiliriz?

Elimizde bir tarih-zaman (datetime) değişkeni olduğunda, yıl, ay, ve gün olarak parçalanan değişkenlere literatürde en çok kullanılan bir-elemanı-bir kodlama (one-hot encoding) yöntemi uygulanır. Bu yöntem kimi zaman iyi cevap verse de bilgi kaybına neden olmaktadır. Saat değişkenine sahip olduğumu varsayalım, bu değişkeni nasıl ele alırdık? Sonuçta girdilerimizin döngüsel yapısını korumak istiyoruz. Aynı zamanda, verinin boyutunu arttırmak istemiyoruz…

Döngüsel verileri kodlamak için yaygın bir yöntem, sinüs ve konsinüs dönüşümü kullanarak verileri iki boyuta dönüştürmektir. Bunu aşağıdaki dönüşümleri kullanarak yapabiliriz:

ve

Burada max(x)üzerinde çalıştığımız döngüsel değişkenin maksimum alacağı değerdir.

Örneğin, saat değişkenimiz olduğunu varsayalım. Burada, saat değişkeni, 24-saat formatına çevrildikten sonra 0 ile 23 arasında değer alır. Böylelikle, max(x) = 23.0 olacaktır. Python ile bu değişkenleri üretmek oldukça kolaydır:

data['hour_sin'] = np.sin(2 * np.pi * data['hour']/23.0)
data['hour_cos'] = np.cos(2 * np.pi * data['hour']/23.0)

İlk olarak, bir zaman değişkeni üretelim. Yalnızca 24 saatlik bir saat üzerinde zamanın nerede göründüğüne baktığımız için, zamanları gece yarısından sonraki saniyeler olarak gösterebiliriz.

%matplotlib inline
import matplotlib.pyplot as plt
plt.style.use('ggplot')
plt.rcParams["figure.figsize"] = (12,8)
import pandas as pd
import numpy as np

def rand_times(n):
    """Generate n rows of random 24-hour times (seconds past midnight)"""
    rand_seconds = np.random.randint(0, 24*60*60, n)
    return pd.DataFrame(data=dict(seconds=rand_seconds))

n_rows = 1000

df = rand_times(n_rows)
# sort for the sake of graphing
df = df.sort_values('seconds').reset_index(drop=True)
df.head(n=10)
#    seconds
# 0	 139
# 1	 245
# 2	 282
# 3	 294
# 4	 354
# 5	 451
# 6	 482
# 7	 518
# 8	 543
# 9	 846

Oluşturduğumuz bu sütunu çizdirdiğimizde elde edeceğimiz grafik şu şekildedir:

plt.figure(0)
df.seconds.plot()
plt.savefig('plot1.png')

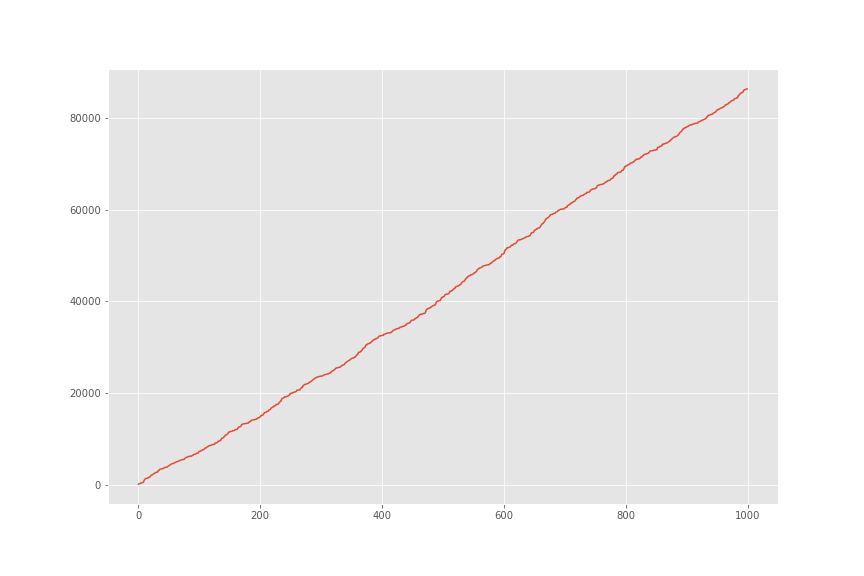
Grafiğin başına ve sonuna bakalım. Gece yarısından 5 dakika öncesi (23:55) ve 5 dakika (00:05) sonrası gibi iki nokta arasındaki mesafenin çok büyük olduğuna dikkat ediniz. Bu istenmeyen bir durumdur: makine öğrenmesi modelimizin 23:55 ve 00:05 arasındaki farkın sadece 10 dakika olduğunu görmesini istiyoruz, ancak bu durumda bu saatler 23 saat 50 dakika arayla görünecektir! İşte bunu elde etmek üzere iki yeni değişken oluşturacağız. Yukarıda oluşturduğumuz gece-yarısından-sonraki-saniye değişkenine sinüs ve kosinüs dönüşümleri uygulayacağız.

seconds_in_day = 24*60*60

df['sin_time'] = np.sin(2*np.pi*df.seconds/seconds_in_day)
df['cos_time'] = np.cos(2*np.pi*df.seconds/seconds_in_day)

df.drop('seconds', axis=1, inplace=True)

df.head()
#	sin_time	cos_time
#0	0.010108	0.999949
#1	0.017816	0.999841
#2	0.020506	0.999790
#3	0.021379	0.999771
#4	0.025741	0.999669

Bu iki değişkeni birlikte 24-saatlik bir saat olarak çizdirirsek aşağıdaki grafiği elde ederiz:

plt.figure(1)
df.sample(50).plot.scatter('sin_time','cos_time').set_aspect('equal');
plt.savefig('plot2.png')

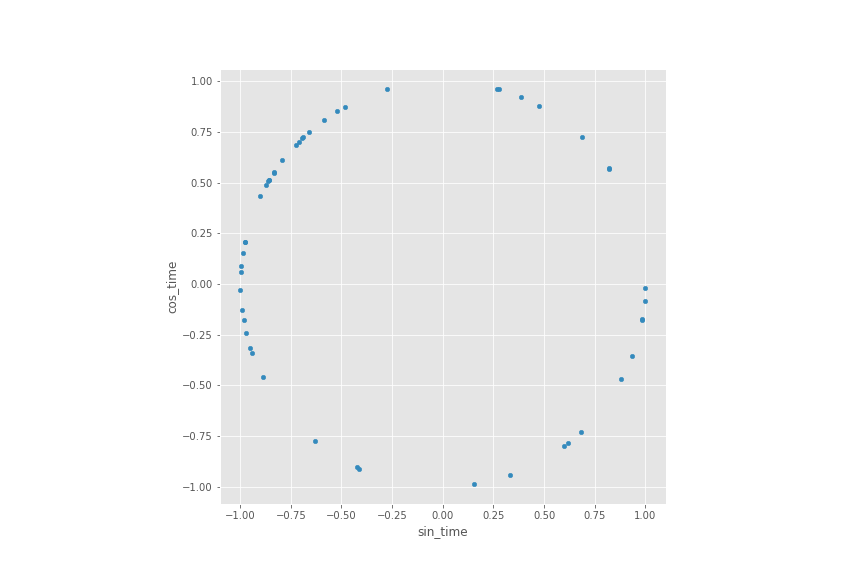
Kolaylıkla görüldüğü üzere, iki nokta arasındaki mesafe, 24 saatlik bir döngüden beklediğimiz gibi zaman farkına karşılık gelir. Artık bu iki değişken makine öğrenmesi modelimiz için rahatlıkla kullanılabilir. Buna ek olarak, değişkenler [-1, 1] aralığına ölçeklendiğinden, herhangi bir şekilde modeli domine etmeyecektir. Ek olarak, sin/cos tekniği bilgileri saat cinsinden korumaktadır (yani 23:00, 21:00’a göre, 00:00’a daha yakındır). Benzer şekilde, bu tekniği haftanın günlerine uyguladığımızda, Pazar gününün Pazartesi’ye daha yakın olduğu bilgisini modelimizde kolaylıkla işleyebiliriz.

Referanslar

1. https://www.avanwyk.com/encoding-cyclical-features-for-deep-learning/
2. http://blog.davidkaleko.com/feature-engineering-cyclical-features.html
3. https://ianlondon.github.io/blog/encoding-cyclical-features-24hour-time/
4. https://stats.stackexchange.com/questions/126230/optimal-construction-of-day-feature-in-neural-networks
5. https://datascience.stackexchange.com/questions/4967/quasi-categorical-variables-any-ideas
6. https://datascience.stackexchange.com/questions/2368/machine-learning-features-engineering-from-date-time-data
7. https://medium.com/ai%C2%B3-theory-practice-business/top-6-errors-novice-machine-learning-engineers-make-e82273d394db
8. https://datascience.stackexchange.com/questions/5990/what-is-a-good-way-to-transform-cyclic-ordinal-attributes